backpropagation
参数化模型
Parameterized models: $\bar{y}=G(x,w)$.
简单来讲,参数化模型就是依赖于输入和可训练参数的函数。 其中,可训练参数在不同训练样本中是共享的,而输入则因每个样本不同而不同。在大多数深度学习框架中,参数是隐性的(implicit):当函数被调用时,参数不被传递。 如果把模型比作面向对象编程,这些参数相当于被“储存在函数中”。
-
变量(张量,标量,连续变量,离散变量)
- $x$是参数模型的输入
- $\tilde{y}$是由函数计算出的变量,这个函数是确定,非随机的。
-
确定性函数: $x\rightarrow G(x,w) \rightarrow \tilde{y}$
- 可以有多个输入和多个输出
- 包含一些隐性的参数变量 $w$
-
标量函数: $\tilde{y}\rightarrow C(y,\tilde{y}\leftarrow y$
- 用来表示代价函数
- 拥有一个隐性的标量输出
- 用多个输入计算出一个值(通常情况下这个值是这几个输入之间的距离)
==深度学习说白了就是围绕着梯度相关方法展开的。==
SGD (随机梯度下降)的参数更新法则:
- 从样本集中$\lbrace 0, \cdots, P-1 \rbrace$里选取一个 $p$ ,进行参数更新: $w \leftarrow w-\eta \frac{\partial L(x[p], y[p], w)}{\partial w}$
Notation summary
| notation | meaning |
|---|---|
| $a_i^l$ | output of a neuron |
| $a^l$ | output vector of a layer |
| $z_i^l$ | input of activation function |
| $z^l$ | input vector of activation function for a layer |
| $w_{ij}^l$ | a weight |
| $W^l$ | a weight matrix |
| $b_i^l$ | a bias |
| $b^l$ | a bias vector |
Layer output relation: from $a$ to $z$
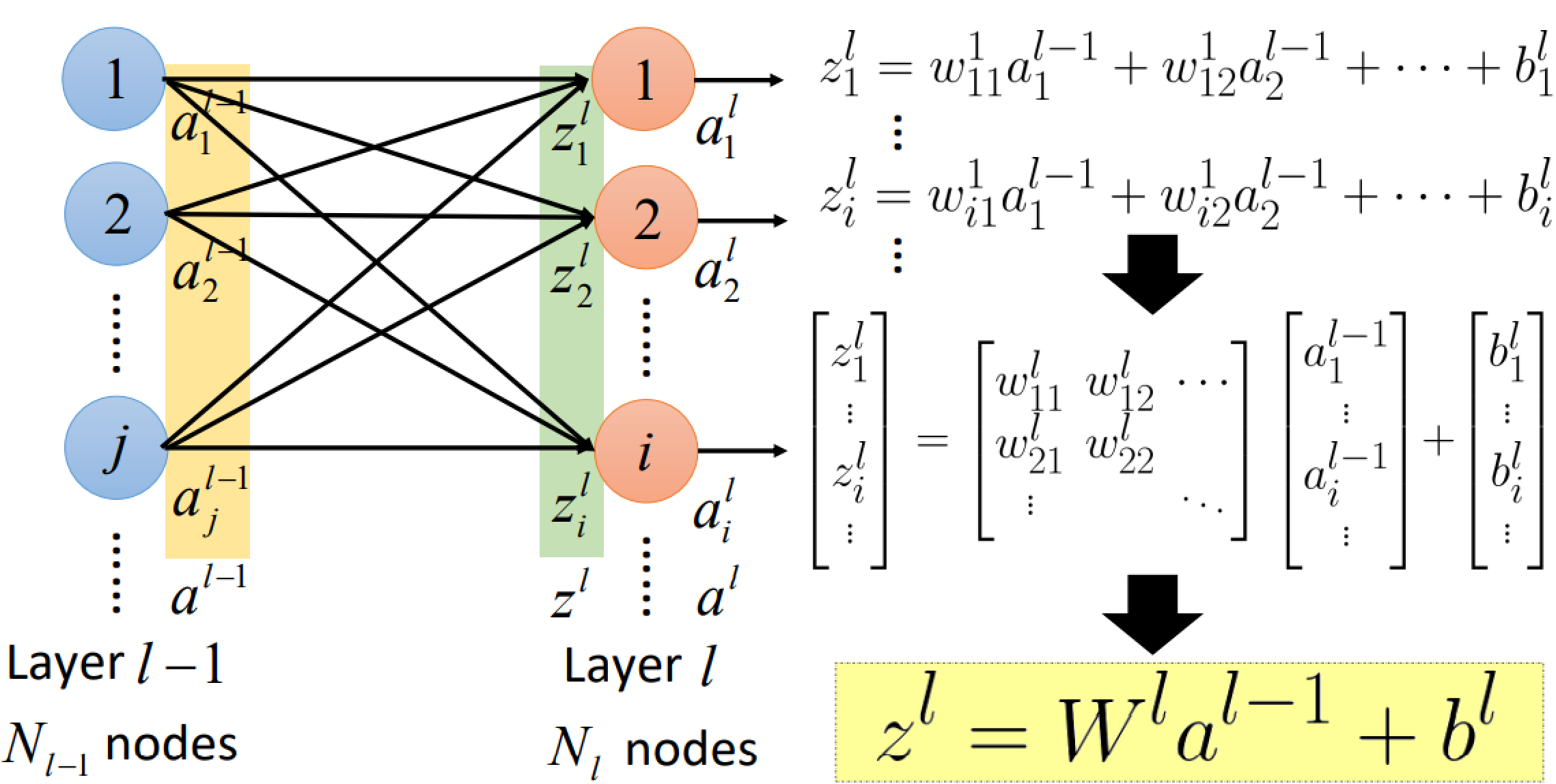
其次,$z_i^l$与$a_i^l$的关系为$a_i^l=\sigma(z_i^l)$,因此有:
$$ \left[\begin{array}{c}a_{1}^{l} \ a_{2}^{l} \ \vdots \ a_{i}^{l} \ \vdots\end{array}\right]=\left[\begin{array}{l}\sigma\left(z_{1}^{l}\right) \ \sigma\left(z_{2}^{l}\right) \ \vdots \ \sigma\left(z_{i}^{l}\right) \ \vdots\end{array}\right]\quad\Rightarrow \quad a^l=\sigma(z^l)=\sigma(W^la^{l-1}+b^l) $$
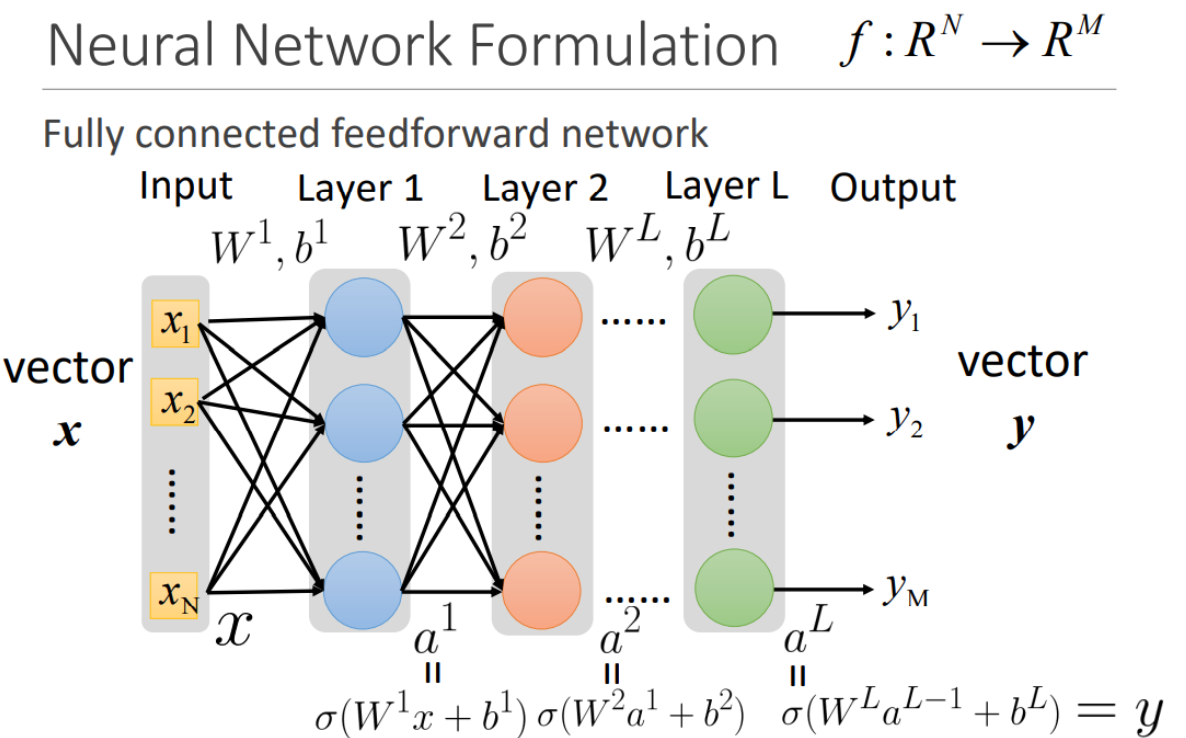
$$ y=f(x)=\sigma\left(W^{L} \cdots \sigma\left(W^{2} \sigma\left(W^{1} x+b^{1}\right)+b^{2}\right) \ldots+b^{L}\right) $$
Loss function for training
- A "Good" function: $f(x ; \theta) \sim \hat{y} \Rightarrow |\hat{y}-f(x ; \theta)| \approx 0$
- Define an example loss function: $C(\theta)=\sum_{k} \left | \hat{y}_{k}-f\left(x_{k} ; \theta \right) \right |$
Gradient Descent for Neural Network

Backpropagation
In a feedforward neural network:
- forward propagation
- from input $𝑥$ to output $𝑦$ information flows forward through the network
- during training, forward propagation can continue onward until it produces a scalar cost $C(θ)$
- back-propagation
- allows the information from the cost to then flow backwards through the network, in order to compute the gradient
- can be applied to any function

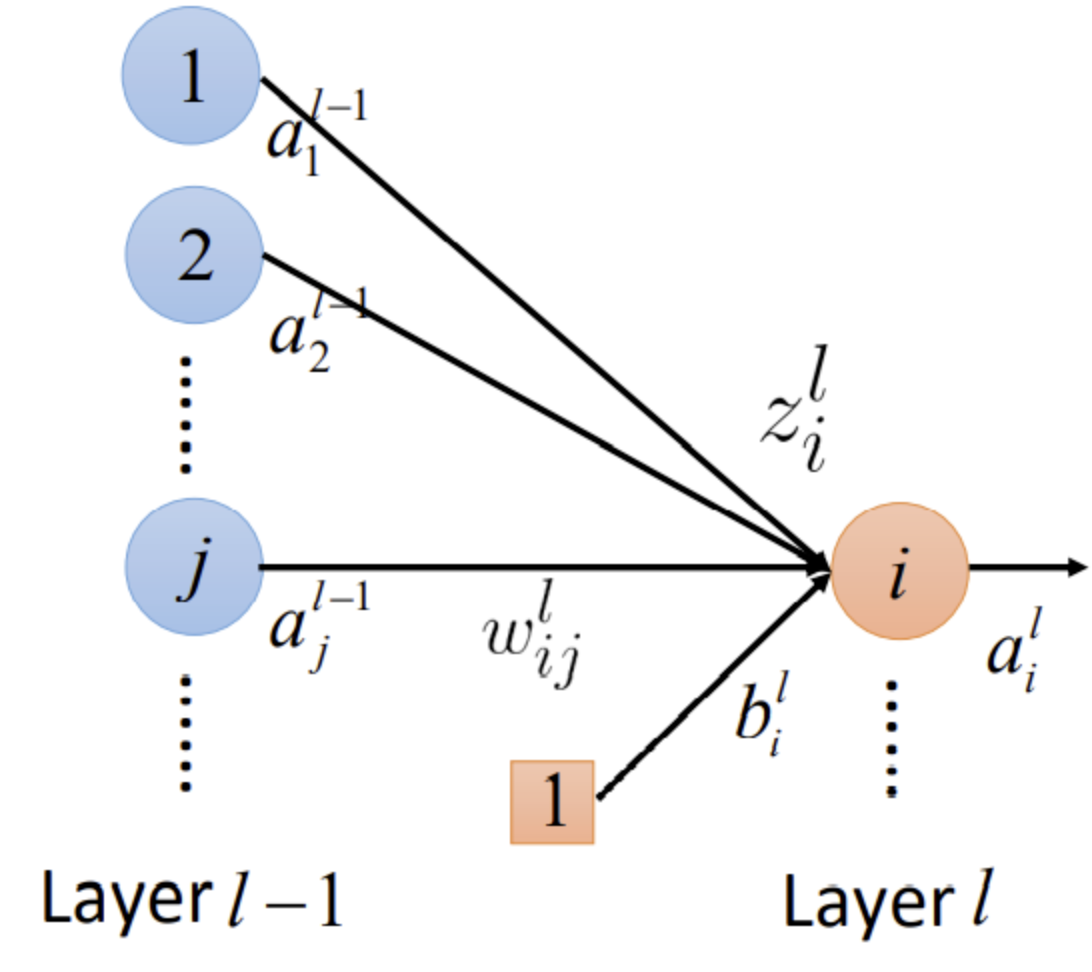
$$ \frac{\partial C(\theta)}{\partial w_{i j}^{l}}=\frac{\partial C(\theta)}{\partial z_{i}^{l}} \frac{\partial z_{i}^{l}}{\partial w_{i j}^{l}} $$
$$ z^{l}=W^{l} a^{l-1}+b^{l} $$
$$ z_{i}^{l}=\sum_{j} w_{i j}^{l} a_{j}^{l-1}+b_{i}^{l} $$
$$ \frac{\partial z_{i}^{l}}{\partial w_{i j}^{l}}=a_{j}^{l-1} $$
$$ \frac{\partial z_{i}^{l}}{\partial w_{i j}^{l}}=\left\{\begin{array}{cl}a_{j}^{l-1} & , l>1 \\ x_{j} & , l=1\end{array}\right. $$
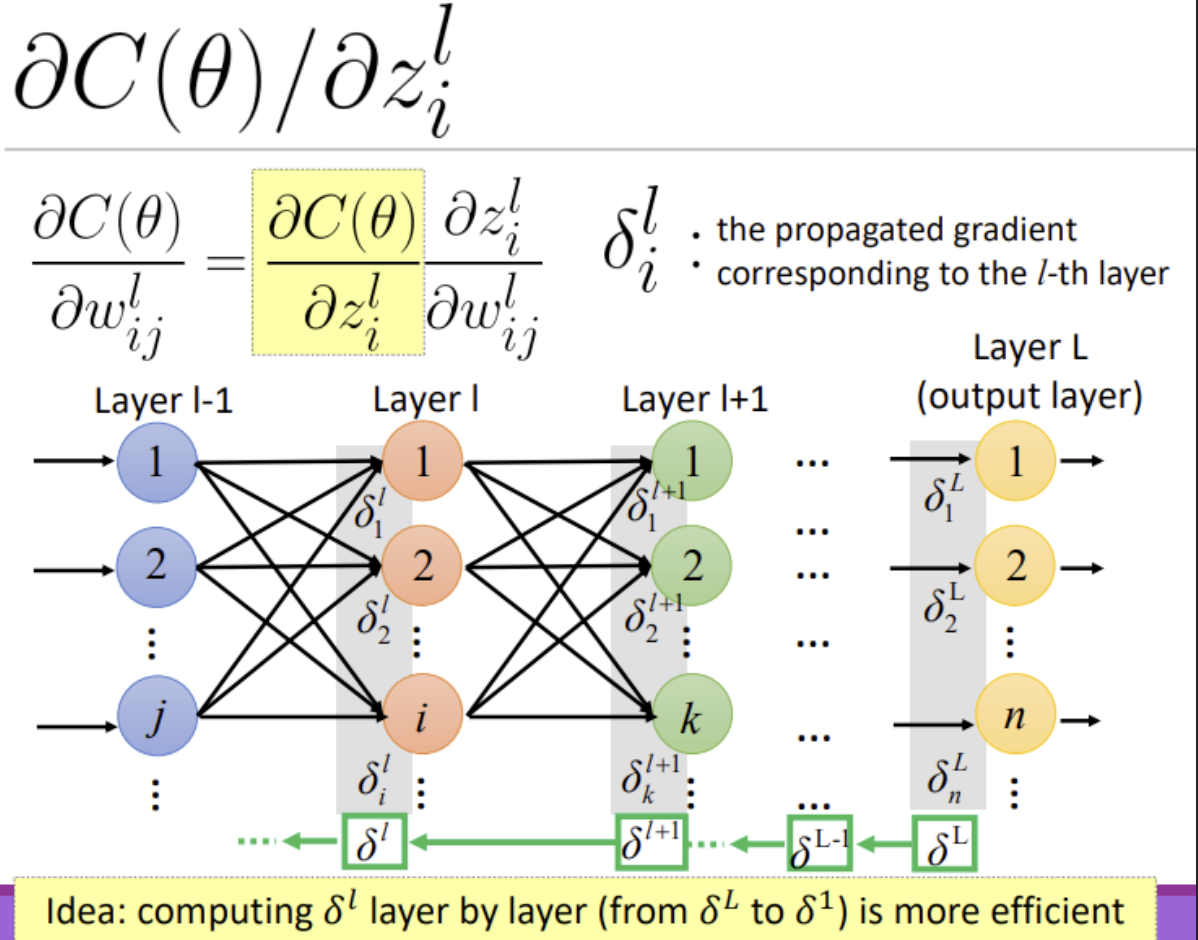
★★★★★ : $\delta_i^l$是第$l$层的传播梯度。直接将这个难求的$\partial{C(\theta)}/\partial{z_i^l}$设为$\delta_i^l$.
Idea: from $L$ to $1$:
- Initialization: compute $\delta^L$
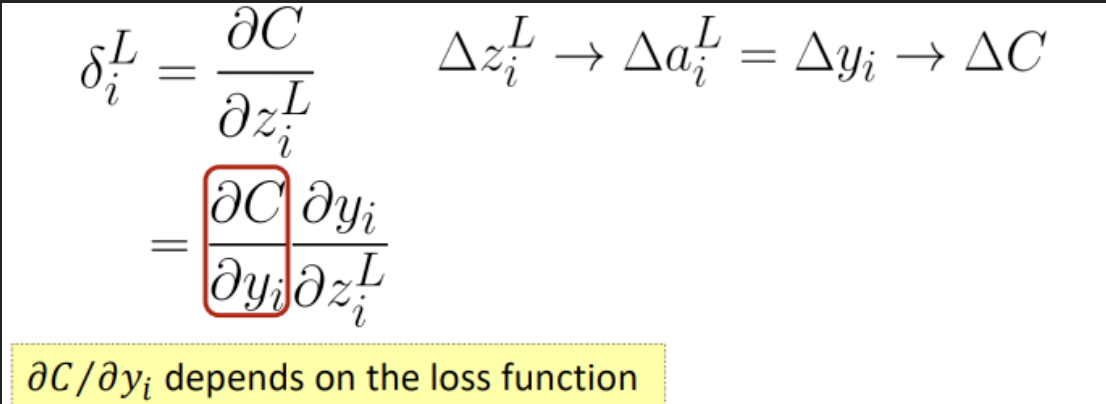

- ★★★★★ : Compute $\delta^l$ based on $\delta^{𝑙+1}$
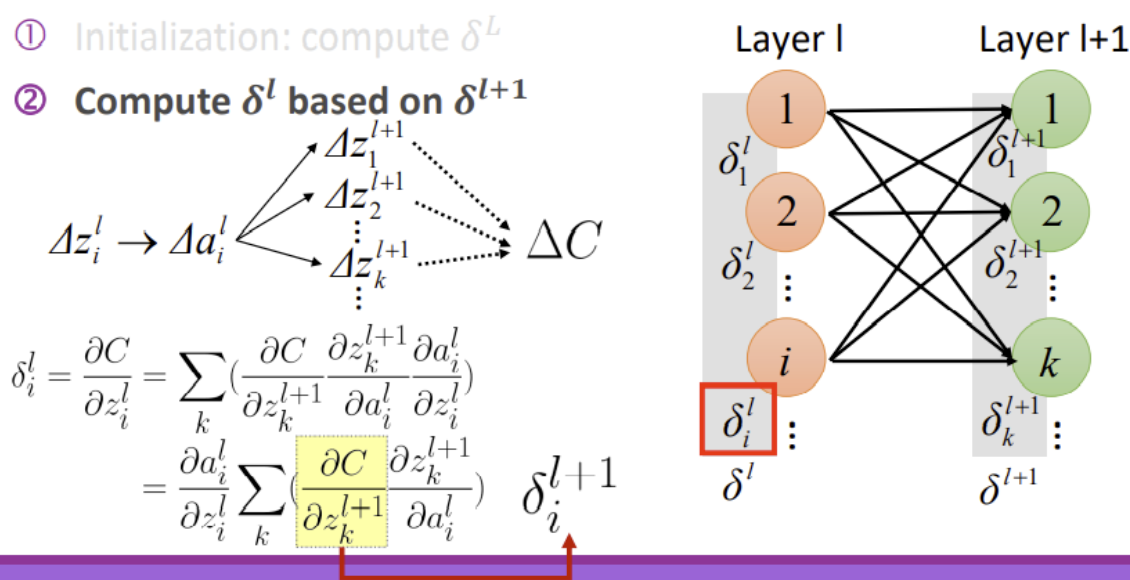

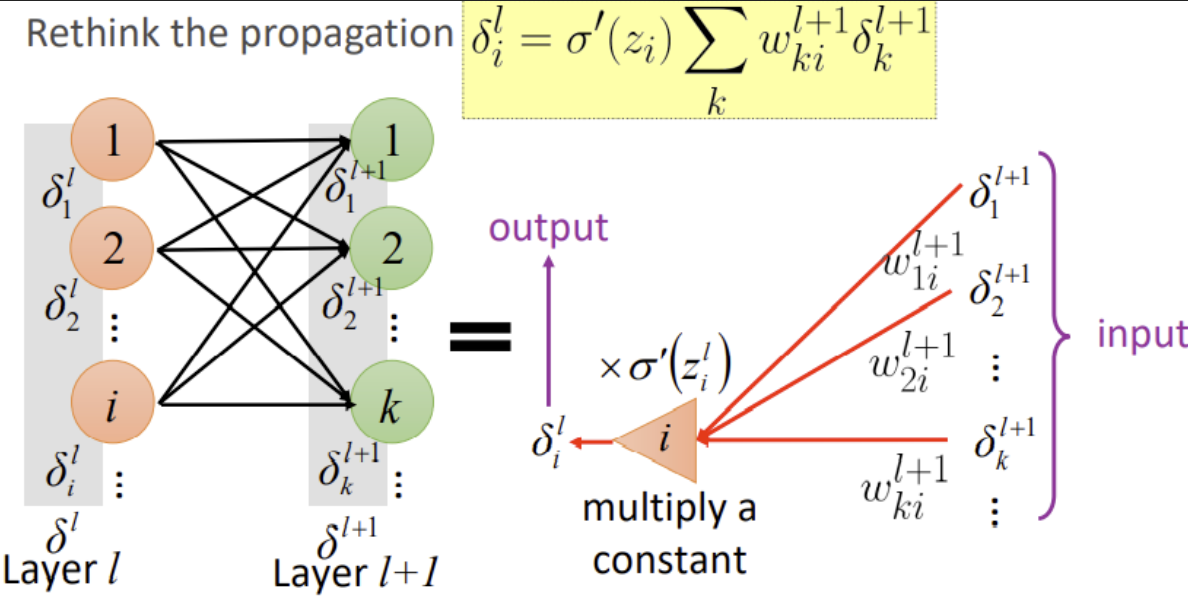
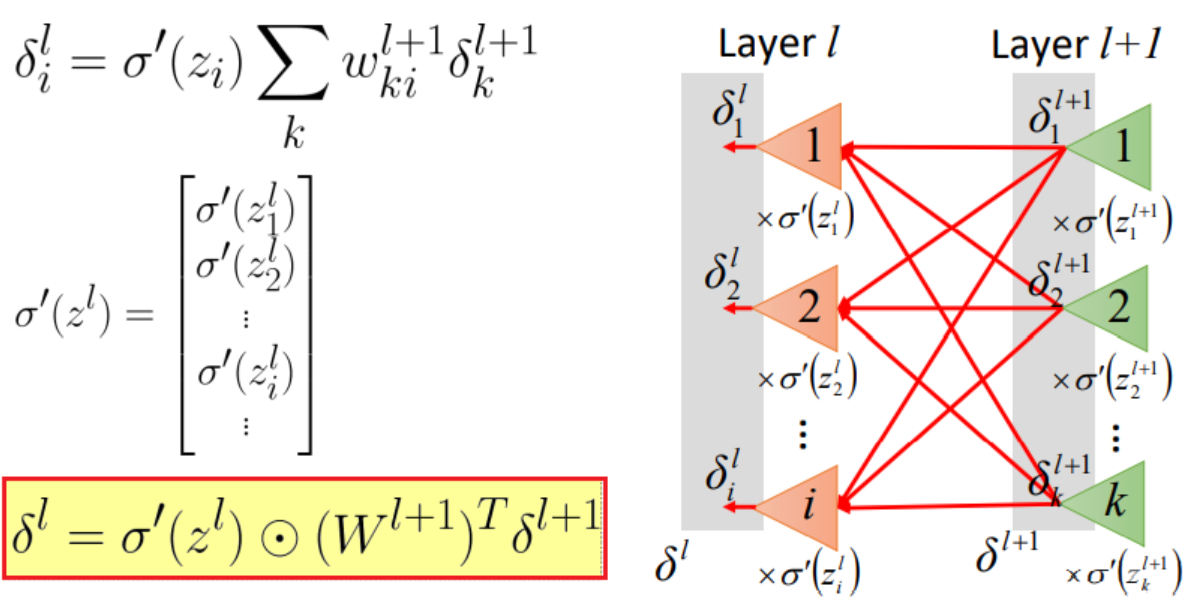
$$ \frac{\partial C(\theta)}{\partial w_{i j}^{l}}={\color{red}{\frac{\partial C(\theta)}{\partial z_{i}^{l}}}} \frac{\partial z_{i}^{l}}{\partial w_{i j}^{l}} $$
★★★★重要
$$ \begin{array}{l} \delta^{L}=\sigma^{\prime}\left(z^{L}\right) \odot \nabla C(y) \ \delta^{l}=\sigma^{\prime}\left(z^{l}\right) \odot\left(W^{l+1}\right)^{T} \delta^{l+1} \end{array} $$
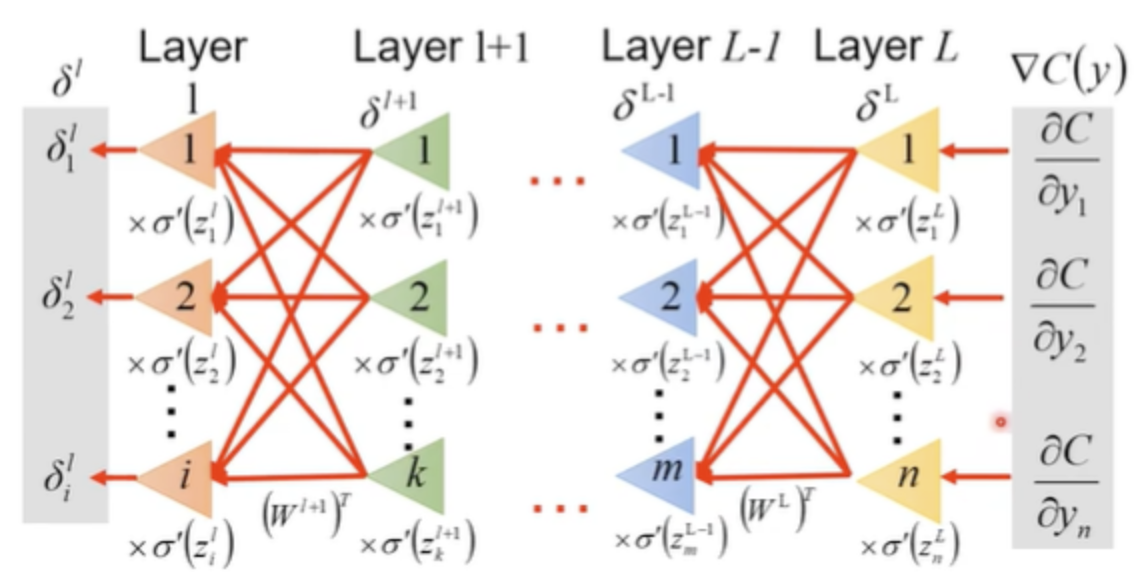
总结
| $\frac{\partial C(\theta)}{\partial w_{i j}^{l}}=\frac{\partial C(\theta)}{\partial z_{i}^{l}} {\color{red}\frac{\partial z_{i}^{l}}{\partial w_{i j}^{l}}}$ | $\frac{\partial C(\theta)}{\partial w_{i j}^{l}}={\color{red}\frac{\partial C(\theta)}{\partial z_{i}^{l}}} \frac{\partial z_{i}^{l}}{\partial w_{i j}^{l}}$ |
|---|---|
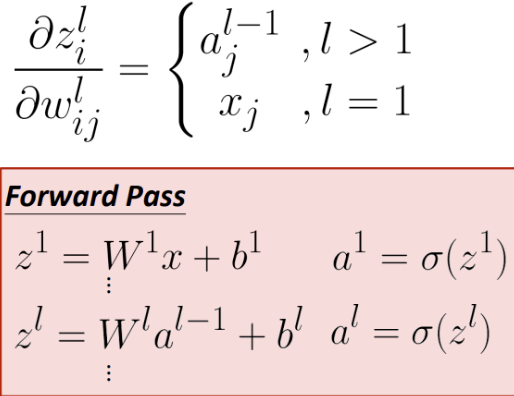 |
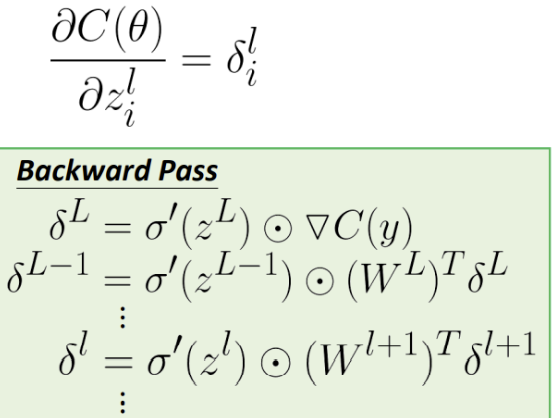 |
向量-雅克比乘积
PyTorch :自动求导.
其他注意事项
- 反向传播不只适用于层层堆叠的模型;它可用于任何有向无环图(DAG)只要模组间具有偏序关系,
Reference
-
李宏毅机器学习课程