Language Modeling

“对xx建模”到底意味着什么？

想象我们有一个物理世界的模型。我们会期待其可以做些什么呢？如果这个模型很好，那么也许它可以根据给定“上下文”(context)的描述来预测下一步会发生什么。而当前的context也就对应着当前事物的状态(state)。

一个好的模型应该能模拟真实世界中的行为,它将“了解”哪些事件与世界更一致，即哪些事件更有可能发生。

那么对于语言呢？

对于语言，这样的直觉是一致的，而不同的是事件的符号。在语言中，一个事件是一个语言单元（例如文本、句子、token、符号），而语言模型的目的是估计出这些事件发生的概率。

Language Models (LMs) estimate the probability of different linguistic units: symbols, tokens, token sequences.

那么语言模型为什么会有用呢？

其实我们每天都在使用语言模型(LMs)! 通常，大型商业服务中的模型比我们今天要讨论的模型要复杂一些，但是思想是一致的。如果我们可以估计单词/句子等的概率，那么我们将有许多意想不到的应用。

然而这件对人类来说容易的事情，对于机器来说可能很难。

当涉及自然语言时，我们人类已经有了“概率”的直觉。例如，当我们谈话时，我们可以很好地理解对方所说的话。我们消除了听起来似乎相似的单词或语句之间的歧义！

但是一个机器应该如何理解这些呢？机器需要语言模型，用来估计句子的概率。如果语言模型足够好，那么它将给正确的句子赋予更大的概率值。

通用框架

文本概率

我们的目的是估计文本片段的概率。简洁起见，假设我们处理的是句子。我们希望这些概率值能翻译对应语言的知识。具体来说，根据语言模型，我们希望在对应语言环境中更有可能出现的句子拥有更大的概率值。

上图的例子中，我们根据经典概率论中频率估计概率的思想，也想使用各种句子在语料中出现的频率来估计其对应的概率。然而这显然不现实，因为我们不可能得到包含所有类型句子的文本语料库。虽然“the mut is tinming the tebn"显然比"mut the tinming tebn is the"更有可能出现，但这些句子的概率估计都为0，即对模型看起来同样糟糕。这意味着这样的模型是不够好的，我们需要进行调整。

将整个句子的概率拆解为一些小的部分

在上述的例子中，我们将句子视为语言的原子单位(atomic units)，因而无法产生可靠的估计概率。那如果我们将句子的概率拆解为一些更小部分的组合呢？

例如，对于一段句子"I saw a cat on a mat", 假设我们是一字一字地阅读这段句子。在每步中，我们估计目前为止所有见到单词的概率。我们不希望有任何计算是徒劳的，因此我们不会在一个新的单词出现就抛弃之前计算的概率值，而是更新这个概率值来解释新的单词。

形式上，令$y_1, y_2, \dots, y_n$表示句子中的单词，$P(y_1, y_2, \dots, y_n)$为目前所见所有单词的概率。通过使用链式法则，这个联合概率可以分解为：

$$ \begin{aligned} P(y_1, y_2, \dots, y_n)&=P(y_1)\cdot P(y_2|y_1)\cdot P(y_3|y_1, y_2)\cdot\dots\cdot P(y_n|y_1, \dots, y_{n-1})\\&= \prod \limits_{t=1}^n P(y_t|y_{\mbox{<}t}). \end{aligned} $$

这样一来，在给定先前上下文的情况下，我们将整个句子的概率分解为每个单词的条件概率。这就是一个标准的从左到右的语言模型。这个框架很通用，N-gram模型和神经网络的语言模型在此框架下，只有计算条件概率$P(y_t|y_1, \dots, y_{t-1})$的方式不同。

使用语言模型生成一个文本

一旦我们有了一个较好的语言模型，我们将可以使用它来生成文本。我们每次生成一个单词或符号，并根据之前生成的文本来预测下一个单词或符号的概率分布，并从该概率分布中抽样：

尽管这种采样方式很简单，但是在文本生成中却经常被用到。

我们可以应用贪婪式的解码，即在每个步骤中，选择概率最高的token。但是，这样做的效果通常不会很好。

N-gram语言模型

原理

让我们回想一下，一般的从左到右的语言建模框架将token序列的概率分解为给定先前上下文的每个token的条件概率乘积：

$$ \begin{aligned} P(y_1, y_2, \dots, y_n)&=P(y_1)\cdot P(y_2|y_1)\cdot P(y_3|y_1, y_2)\cdot\dots\cdot P(y_n|y_1, \dots, y_{n-1})\\ &= \prod \limits_{t=1}^n P(y_t|y_{\mbox{<}t}). \end{aligned} $$

而唯一不确定的是如何计算这些条件概率。因此，我们所要做的就是定义计算这些条件概率的方法。

与之前Word Embeddings中基于计数的方法非常相似，N-gram语言模型也采用计算文本语料中的全局统计信息建模，即通过计数的方法。也就是说，N-gram语言模型估计概率$P(y_t|y_{\mbox{<}t}) = P(y_t|y_1, \dots, y_{t-1})$的方法几乎等价于之前我们基于古典概率论中频率估计概率的方法(文本概率)。

这里突出了“几乎”二词是因为N-gram模型还包含了两个非常重要的成分：马尔科夫性质和平滑方法。

马尔科夫性质（独立假设）

计算$P(y_t|y_1, \dots, y_{t-1})$一种方法：

$$ P(y_t|y_1, \dots, y_{t-1}) = \frac{N(y_1, \dots, y_{t-1}, y_t)}{N(y_1, \dots, y_{t-1})}, $$

其中$N(y_1, \dots, y_k)$代表token序列$(y_1, \dots, y_k)$在文本中出现的频数。

这个方法之前也讨论过，因为片段$(y_1, \dots, y_{t})$在语料中都没有出现，因此该方法效果不会太好。为了解决这个问题，引入了独立性假设，即马尔科夫性质成立：

The probability of a word only depends on a fixed number of previous words. 一个词出现的概率只取决于之前固定长度的单词。

形式上，N-gram模型假设： $$ P(y_t|y_1, \dots, y_{t-1}) = P(y_t|y_{t-n+1}, \dots, y_{t-1}). $$ 例如：

N=3时(trigram model)： $P(y_t|y_1, \dots, y_{t-1}) = P(y_t|y_{t-2}, y_{t-1})$
N=2时(bigram model): $P(y_t|y_1, \dots, y_{t-1}) = P(y_t|y_{t-1})$
N=1时(unigram model): $P(y_t|y_1, \dots, y_{t-1}) = P(y_t)$

下图显示了使用该假设前后的对比：

平滑：重新分配概率质量（Redistribute Probability Mass）

假设我们使用的是4-gram语言模型，并思考如下例子：

如果上式中分子为0或分母为0怎么办呢？这两种情况显然都对模型不友好。为了避免这种情况，通常的做法是使用平滑方法。平滑方法将重新分配概率质量，即将一些存在的事件的概率质量分一些给未出现的事件。

当分母出现频数为0时，即"N(cat on a)=0"

方案一：后退法(aka Stupid Backoff)。Backoff的思想是对于那些未出现的序列，我们只使用其子序列的频数估计。举例来说，对于"cat on a"这是一个trigram模型，如果"cat on a"没有出现，则将其退化为使用bigram模型，即计算"on a"的频数；若还是没有出现，则再退化使用unigram模型。

这种方法看起来傻乎乎的，但实际上却效果还可以。

另一种更聪明的方法是：线性插值(Linear interpolation)。线性插值将使用unigram、bigram、trigram等的结合。为了做到这点，需要使用一些正的权重标量$\lambda_0, \lambda_1, \dots, \lambda_{n-1}$，并且满足$\sum\limits_{i}\lambda_i=1$。如此，更新的概率将为：

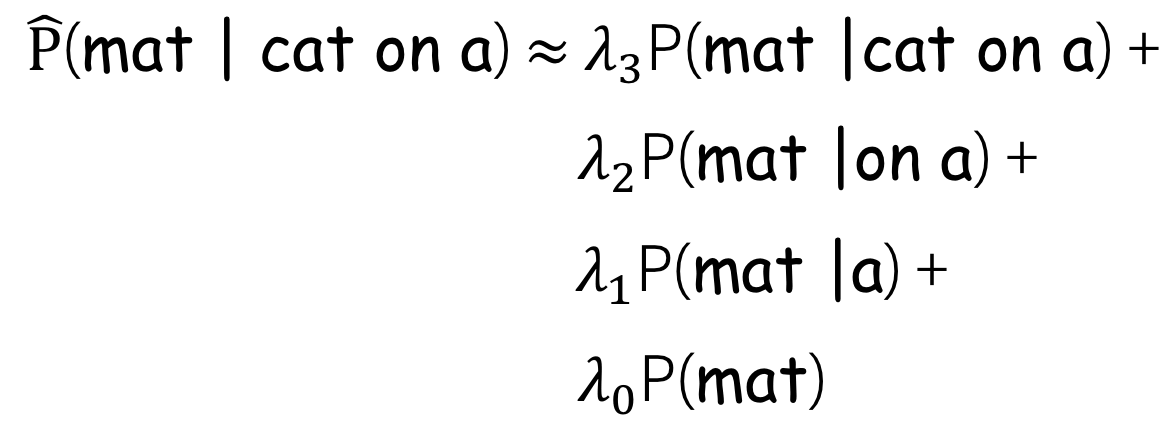
权重系数$\lambda_i$可以使用交叉验证来选择。

当分子为0时，即"N(cat on a mat)=0"

这种情形下，常用的方法是拉普拉斯平滑（aka 加1平滑， add-one smoothing）。避免这种情况最简单的方法是假设每个n-grams都至少出现1次，即每个n-grams的计数都加上1，或者加上一个很小的值 $\delta$:

生成文本

N-gram模型生成文本的过程与使用语言模型生成一个文本]中的通用过程相似：

给定当前的历史上下文
生成下一个token的概率分布
从概率分布中抽样一个token,并将其加入到序列中
重复上述步骤

唯一不同的地方在于条件概率的计算：

生成文本的例子

下面展示一个3-gram模型在250w条英语句子中训练的结果：

在上述的例子中，你可能发现这些句子中不是很流畅。显然，这样的模型没有完全利用到整个语料，而只依赖一小部分的token。而无法充分利用长上下文正是n-gram模型的缺点。

现在，我们仍使用相同的模型，不过利用贪婪式的方法解码：在每一步，我们都选择概率最高的token作为输出。

可以发现贪婪式的解码结果有如下性质：

生成的文本更短： _eos_ token具有很高的输出概率
更加相似：许多文本最终生成的短语是相似的

N-gram语言模型固定上下文所带来的缺点，不会传递给神经网络的语言模型。

神经语言模型

原理

再次重复：计算token序列的概率，需要估计条件概率$P(y_t|y_1, \dots, y_{t-1})$

$$ \begin{aligned} P(y_1, y_2, \dots, y_n)&=P(y_1)\cdot P(y_2|y_1)\cdot P(y_3|y_1, y_2)\cdot\dots\cdot P(y_n|y_1, \dots, y_{n-1})\\&= \prod \limits_{t=1}^n P(y_t|y_{\mbox{<}t}). \end{aligned} $$

不同于N-gram模型是基于全局语料的统计信息来估计条件概率，神经模型通过训练一个网络来预测这些概率。

直觉上，神经语言模型需要做两件事情：

处理上下文-> 对上下文编码(encode context)
1. 主要的思想是获得之前的上下文的词嵌入表示
2. 通过使用该表示，模型预测下一个token的概率分布
3. 这个步骤主要依赖于模型使用的网络架构，例如RNN、CNN等
生成下一个token的概率分布
1. 一旦上下文经过编码，通常下一个token的条件分布可以使用相同方法获得

从上图的流程可以发现，其实神经语言模型就是一个神经分类器，而预测下一个词的概率分布其实就是一个分类问题的一部分。

高层次的Pipeline

由于从左到右的神经语言模型可以被认为是一种分类器，一个通用的pipeline与我们在Text Classification的原理中看到的很相似。对于不同的网络架构，一个通用的pipeline如下：

将之前上下文所有词的词嵌入传给网络
通过训练网络，获得整个上下文的向量表示
根据该向量表示，预测下一个token的概率分布

我们可以先思考分类部分，即如何从文本的向量表示中获取token的概率分布。

假设文本的向量表示的维度为$d$,但最后我们需要一个大小为$|V|$的向量来表示$|V|$个tokens(类别)的概率。为此，我们需要使用一个线性网络层，一旦我们获得了大小为$|V|$的向量，就可以对其使用softmax操作，将原始数值转换为各个类别的概率了。

另一种视野：输出词向量的点积

如果我们仔细观察最后一层线性层，我们将发现其包含$|V|$个列，并且每一列对应着词表中的一个token。因此，这些列向量可以看做是输出词的词嵌入。

使用最后的线性层其实等价于对上下文的向量表示$h$和输出词的词嵌入之间做点积。

形式上，假设$\color{#d192ba}{h_t}$表示上下文$y_1, \dots, y_{t-1}$的向量表示，$\color{#88bd33}{e_w}$表示输出词的词嵌入，则输出词的条件概率为： $$ p(y_t| y_{\mbox{<}t}) = \frac{exp(\color{#d192ba}{h_t^T}\color{#88bd33}{e_{y_t}}\color{black})}{\sum\limits_{w\in V}exp(\color{#d192ba}{h_t^T}\color{#88bd33}{e_{w}}\color{black})}. $$

点积作为两个向量相似度的一种度量方式，如果输出词的词嵌入$\color{#88bd33}e_{y_t}$与上下文的向量表示$\color{#d192ba}h_t$的点积越大，即相似度越大，则对应的条件概率也越大。

训练与交叉熵损失

令$y_1, \dots, y_n$表示需训练得到的序列，在时间步$t$上，模型需要预测概率分布$p^{(t)} = p(\ast|y_1, \dots, y_{t-1})$。假设该时间步的目标分布(标签)是$p^{\ast}=\mbox{one-hot}(y_t)$,即我们希望给正确的token$y_t$赋予概率值1，其余为0。

标准的损失函数为交叉熵损失。目标概率分布$p^*$与预测分布$p$之间的损失为： $$ Loss(p^{\ast}, p^{})= - p^{\ast} \log(p) = -\sum\limits_{i=1}^{|V|}p_i^{\ast} \log(p_i). $$ 由于$p^{\ast}$中只有一个元素$p_i^{\ast}$不为0，因此我们可以将上式化简： $$ Loss(p^{\ast}, p) = -\log(p_{y_t})=-\log(p(y_t| y_{\mbox{<}t})). $$

上述损失函数最小化等价于在每个时间步，使模型预测出正确的token的概率最大化。

对于整个序列，损失函数将为$-\sum\limits_{t=1}^n\log(p(y_t| y_{\mbox{<}t}))$。如下以RNN网络为例，展示了训练过程：

交叉熵与KL散度：

当目标分布为独热向量$p^{\ast}=\mbox{one-hot}(y_t)$时，交叉熵损失为$Loss(p^{\ast}, p^{})= -\sum\limits_{i=1}^{|V|}p_i^{\ast} \log(p_i)$,等价于Kullback-Leibler divergence $D_{KL}(p^{\ast}|| p^{})$。

因此，标准的NN-LM优化问题可以被看作是最小化模型预测分布$p$和经验目标分布$p^{\ast}$之间的距离。

模型：循环架构

该小节将介绍用于语言模型的RNN模型。本小节的RNN单元可以使用任意RNN结构，如LSTM，Vanilla RNN, GRU等。

单层 RNN

最简单的循环架构就是单层的循环神经网络。在每个时间步，当前的状态将包含之前tokens的信息，并且将其用于预测下一个token。在训练时，将训练样本传给网络。在推断时，模型将生成一个token。以上步骤直到网络生成_eos_为止。

多层 RNN

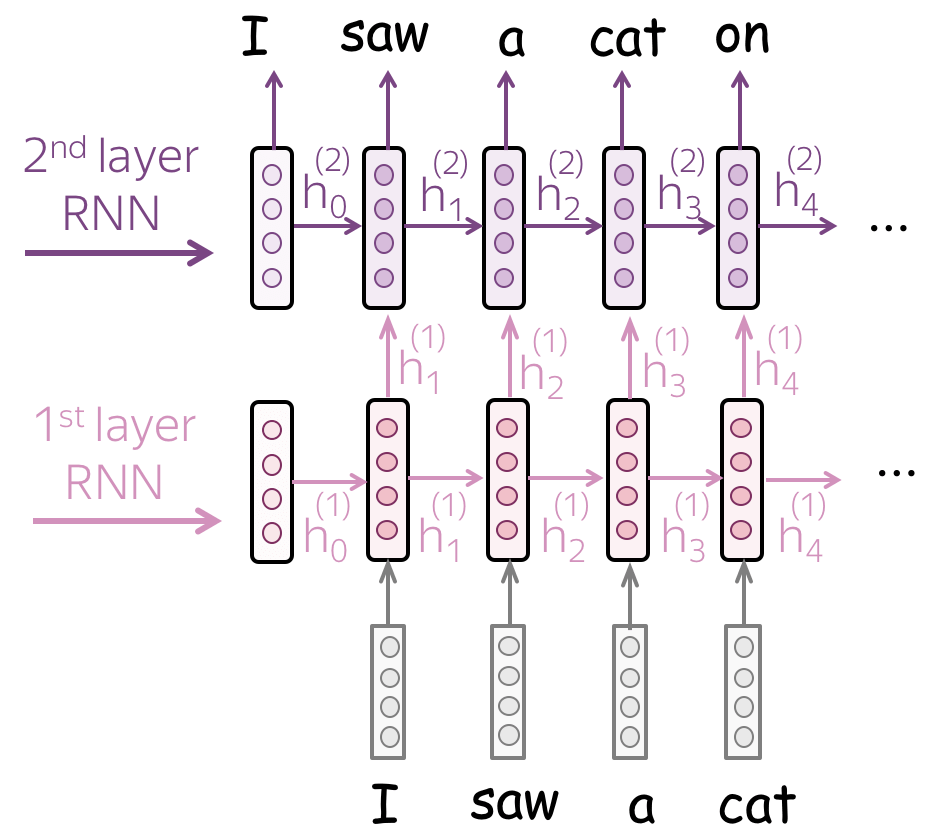
模型：卷积

对比文本分类中的将卷积用于文本的原理,在语言模型中的CNN将有些不同。

当设计CNN语言模型时，我们需要记住如下几点：

防止之前上下文的信息从将来的tokens中溜走
1. 为了预测一个token，一个从左到右的语言模型必须使用之前的tokens，因此我们需要确保CNN只能看到之前上下文的tokens
2. 在最初预测token时，可能之前的上下文长度不够，此时可以添加一些paddings,但是记住不能使用后续tokens
不要移除位置信息
1. 与文本分类不同，位置信息对语言模型非常重要
2. 因此，在CNN语言模型中不要使用池化操作（丢失位置信息）
如果需要堆叠很多层，不要忘记使用残差连接(residual connections)
1. 如果堆叠太多层，则深层的网络将会很难学习
2. 为了避免上述问题，可以使用残差连接与高速连接

感受野(Receptive field): 有了许多层，感受野范围可以很广

当不使用全局池化操作的CNN模型时，我们的模型可能无法避免地使用一个固定大小的上下文窗口，而这正是N-gram模型的缺点，以及我们想极力避免的问题。

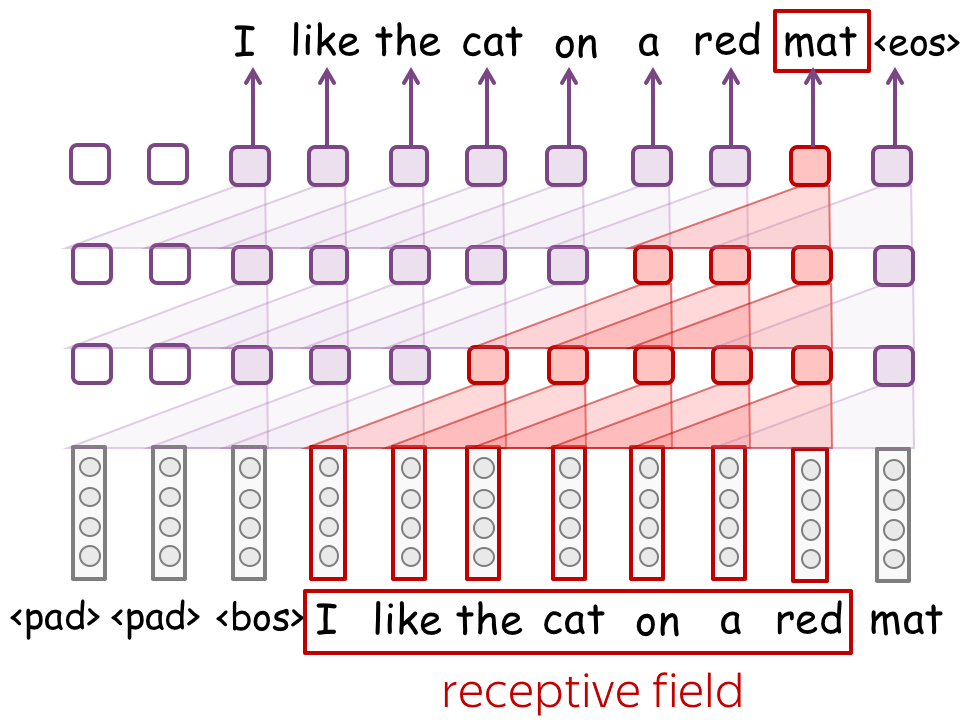
然而，如果N-gram模型的上下文大小通常为1-4,那么CNN模型的上下文大小却可以非常大。在上图中，我们只是用了3层的卷积层，以及过滤器大小为3，但网络却可以接受7个tokens组成的上下文窗口的信息。如果我们继续堆叠更多层，那么我们将可以获得一个非常大的上下文长度。

残差连接：使得训练深层网络更容易

为了处理更长的上下文，我们需要更深的网络。然而不幸地是，当堆叠许多网络层后，我们可能面临深层网络的梯度从顶端网络层很难反向传播到底端网络层。为了避免这个问题，我们可以使用残差连接或者更复杂的变种高速连接(highway connections)。

残差连接非常简单：相对于一般的深层网络，添加了一个输入层到输出层的连接。而高速连接的动机相同，但使用了一个门控来控制输入、输出的和，而不是简单地使用累加和。这与LSTM使用不同的门控控制学习的信息相似。

下图是带有残差连接的CNN模型图例。加入残差连接后，即使网络层数很深，也可以很容易地训练。此外，深层的网络也给模型带来一个非常可观的感受野。

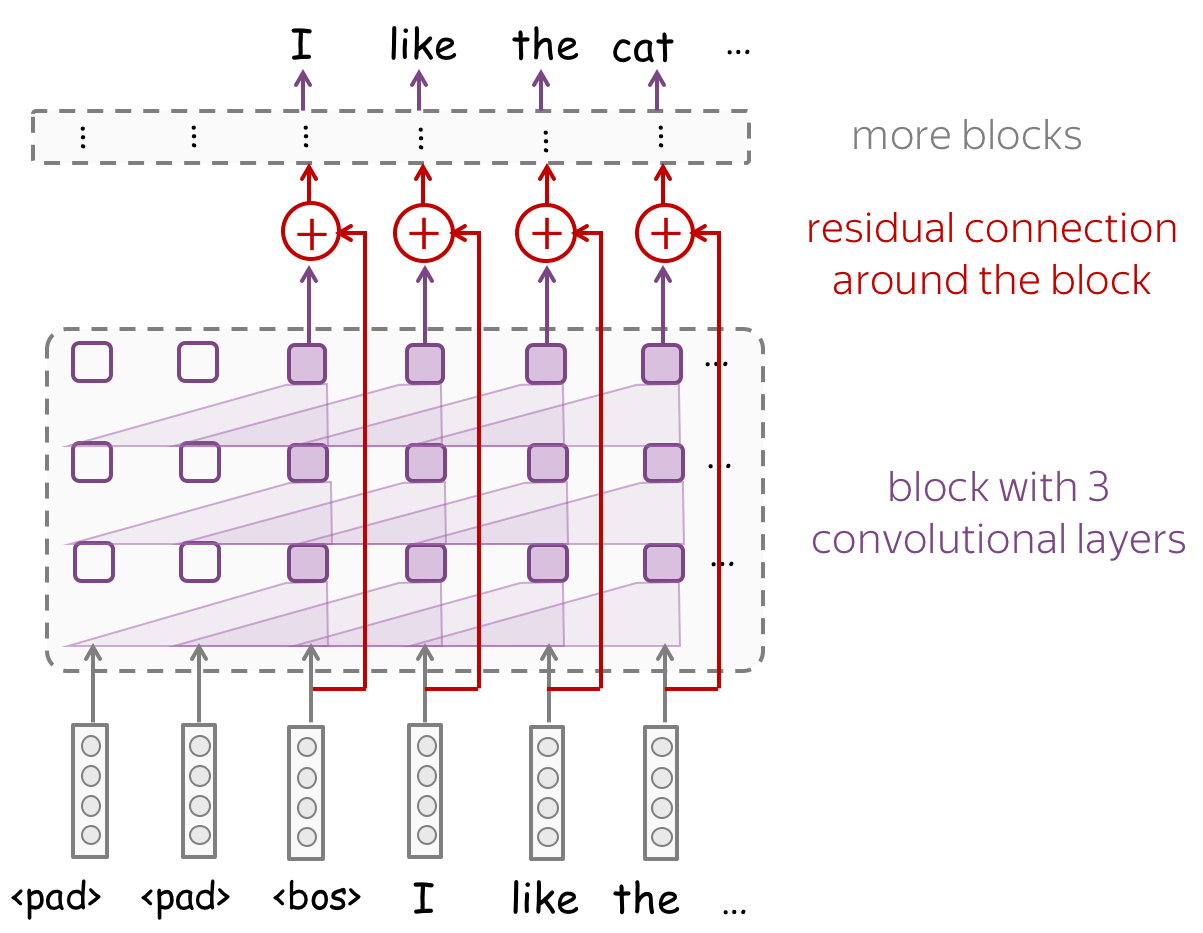
序列生成策略

原理

为了通过语言模型生成一段文本，我们需要从模型预测得到的概率分布中对token抽样。

连贯性和多样性(Coherence and Diversity)

连贯性Coherent: 生成的文本需要讲得通
多样性Diverse: 模型应该能够生成各种各样的句子

标准抽样

生成序列的最标准方法是直接使用模型预测的分布，而不做任何修改。

带温度取样（temperature）

一种非常流行的修改语言模型生成行为的的方法是更改softmax温度。在使用最终的softmax函数之前，softmax函数的输入先除以一个温度值$\tau$。

形式上，softmax的计算发生如下改变：

注意到，采样过程仍然是标准抽样的：唯一不同的是我们计算概率的方式。

实验中，先采取温度范围为$[0.2, 2]$取样。当$\tau=2$时，产生的文本具有很好的多样性，但大多数都没有什么意义。如果换个方向降低温度，例如$\tau=0.2$，此时发现产生的文本虽然更能说的通，但是却大大降低了多样性。为了总结这个发现，我们可以使用温度$\tau$来控制生成文本的连贯性和多样性：

Top-K采样：选择前K个概率最高的tokens

调整温度非常棘手：如果温度设置太低，那么所有的token的概率都会很低（相对而言，即概率值之间相差较大，大的概率很大，小的概率可能接近0）；如果温度太高，则大量的token都将有很高的概率（相对而言，即每个概率值都差不多）。

一种简答的启发式解决方法是总是从概率值最大的K个tokens中取样。在此情况下，模型虽然有K种选择，但是那些最不可能的token将不会被使用到。

然而固定的$K$不总是好的。虽然通常top-K采样比单独使用softmax + temperature的效果好，但固定的K值肯定不是最佳方案。例如下图，

正如上图所示，当$K$值固定时，采样前$K$个token，其中可能包含一些概率值非常小的token(右图所示)。此外，当$K$值固定时，概率大的$K$个token可能对应的含义完全不同（例如左图所示，red,white等完全不同的颜色）。

Top-p%(aka Nucleus)采样：概率质量的前p%

一个更合理的策略是不考虑概率值top-K的tokens，而是考虑概率质量和top-p%的tokens,这个方法称为Nucleus抽样。使用Top-p%采样，网络可以基于概率分布的性质，动态地选择tokens的数量。

评估语言模型

TL;DR : 当"阅读"一段新的文本时，语言模型会有多”惊讶“？

正如在词嵌入表示的评估中所提的，有两种评估语言模型的方法——内部任务评价（Intrinsic Evaluation）和外部任务评价（extrinsic evaluations）。这里仅讨论内部任务评价方法。

类似于物理世界中的好模型必须与现实世界很好地吻合，好的语言模型也必须与真实文本很好地吻合。这是评价方法的主要思想：如果我们输入给模型的文本与模型“期待”得到的文本是接近的，那么这就是个好模型。

交叉熵与困惑度

我们应该如何评估一段文本是否正是模型所期待的呢？形式上，一个模型需要给真实文本赋予高概率，而不太可能出现的文本赋予低概率。

假设我们有一段文本$y_{1:M}= (y_1, y_2, \dots, y_M)$。语言模型赋予这段文本的概率表征了模型与文本“一致”的程度，即语言模型根据给定的上下文预测即将出现的tokens的好坏：

这是一个对数似然函数,但与交叉熵损失函数不同，其没有负号。此外，注意到在训练阶段损失函数中，对数函数的底数取的是$e$，这更容易计算；而在评估阶段的对数函数中，底数取的是$2$。

除了交叉熵函数，更常见的评估方式是交叉熵函数的变形——困惑度(perplexity): $$ Perplexity (y_{1:M})=2^{-\frac{1}{M}L(y_{1:M})}. $$

一个号的模型应该有更高的对数似然函数值，以及更低的困惑度。

最好的困惑度为$1$

假设我们的模型是完美的，每次给正确的tokens的预测概率都是$1$,则此时对数概率值即为$0$,因而困惑度为$1$。

最坏的困惑度为$|V|$

在最糟糕的情况中，语言模型对文本一无所知，因此对文本中的每个token都赋予相同的概率值$\frac{1}{|V|}$,于是：

$$ \begin{aligned} Perplexity(y_{1:M})=2^{-\frac{1}{M}L(y_{1:M})} &= 2^{-\frac{1}{M}\sum\limits_{t=1}^M\log_2 p(y_t|y_{1:t-1})}\\ &= 2^{-\frac{1}{M}\cdot M \cdot \log_2\frac{1}{|V|}}=2^{\log_2 |V|} =|V|. \end{aligned} $$

因此，模型的困惑度取值应在$[1,|V|]$之间。