Seq2Seq模型
由来
在⾃然语⾔处理的很多应⽤中,输⼊和输出都可以是不定⻓序列。以机器翻译为例,输⼊可以是⼀段不定⻓的中文⽂本序列,输出可以是⼀段不定⻓的英语⽂本序列。
当输⼊和输出都是不定⻓序列时,我们可以使⽤编码器-解码器架构(encoder-decoder)或者seq2seq模型。
序列到序列模型,简称seq2seq模型。
这两个模型本质上都⽤到了两个循环神经⽹络,分别叫做编码器和解码器。
- 编码器⽤来分析输⼊序列
- 解码器⽤来⽣成输出序列。
两个循环神经网络是共同训练的。
编码器-解码器图示
在训练数据集中,我们可以在每个句⼦后附上特殊符号“<eos>”(end of sequence)以表⽰序列的终⽌。
编码器每个时间步的输⼊依次为输入句⼦中的单词、标点和特殊符号“<eos>”。
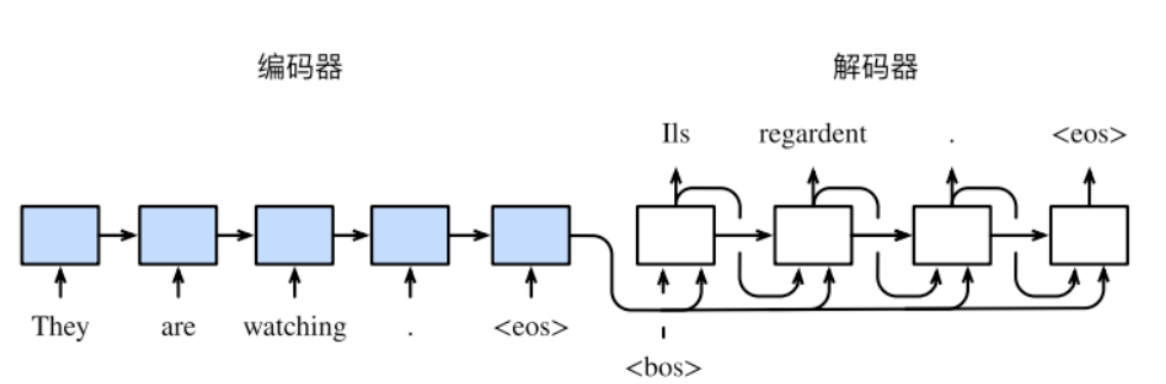
在前向传播训练过程中,编码器在最终时间步的隐藏层状态将会作为输⼊句⼦的表征或编码信息供给后续的解码器使用。将编码器输出的编码信息记为$h^T$。
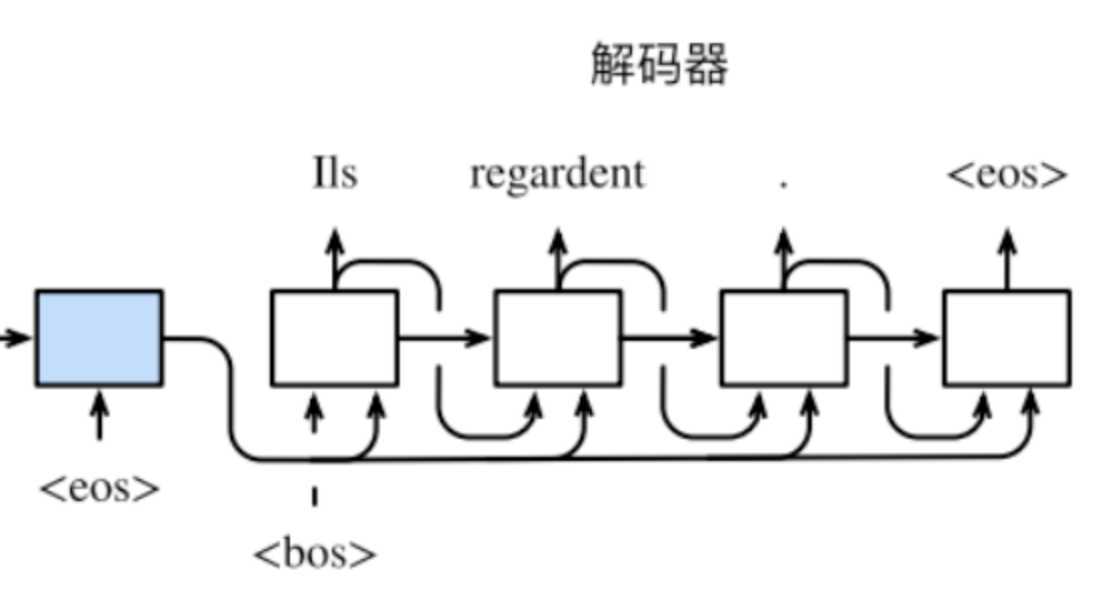
解码器在各个时间步中将使用到如下数据作为输入:
- 使⽤输⼊句⼦的编码信息h^T
- 上个时间步的隐藏层状态
- 上个时间步的输出
我们希望解码器在各个时间步能正确依次输出翻译后的英语单词、标点和特殊符号“<eos>”。
需要注意的是,解码器在最初时间步的输⼊⽤到了⼀个表⽰序列开始的特殊符号“
<bos>”(beginning of sequence)。
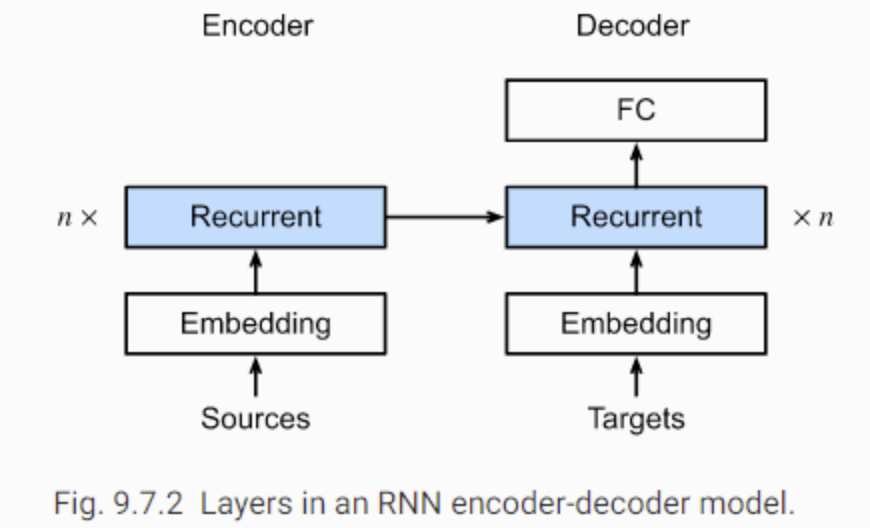
编码器
编码器的作⽤是把⼀个不定⻓的输⼊序列变换成⼀个定⻓的背景变量$C$。该背景变量将会存储输⼊序列的编码信息。常⽤的编码器是循环神经⽹络。
让我们考虑批量⼤小为$1$的时序数据样本。假设输⼊序列是$x_1, . . . , x_T$,例设$x_t$是输⼊句⼦中的第$t$个词。在时间步$t$时刻,循环神经⽹络将输⼊$x^t$的特征向量$\mathbf{x}^t$,以及上个时间步的隐藏状态$h_{t-1}$变换为当前时间步的隐藏状态$h_t$。若使用函数f表达循环神经⽹络隐藏层的变换,则有$h_t=f(\mathbf{x}^t,h_{t-1})$。
接着,编码器通过⾃定义函数$q$将各个时间步的隐藏状态变换为上下文变量(context variable) :$c=q(h_1,...,h_T)$。例如,当选择$q(h_1, . . . ,h_T) =h_T$时,上下文变量是输⼊序列最终时间步的隐藏状态$h^T$。
以上描述的编码器是⼀个单向的循环神经⽹络,每个时间步的隐藏状态只取决于该时间步及之前的输⼊⼦序列。我们也可以使⽤双向循环神经⽹络构造编码器。在这种情况下,编码器每个时间步的隐藏状态同时取决于该时间步之前和之后的⼦序列(包括当前时间步的输⼊),并编码了整个序列的信息。
解码器
编码器的输出--上下文变量$c$是对整个输入蓄力$x_1,...,x_T$编码后的结果。给定训练样本中的输出序列$y_1, y_2, . . . , y_{T'}$,在每个时间步$t^′$上(符号与输⼊序列或编码器的时间步$t$有区别),解码器输出$y_{t^′}$的条件概率将基于解码器之前时间步的输出序列$y_1,...,y_{t'-1}$和背景变量$c$,即:
$$ P\left(y_{t^{\prime}} \mid y_{1}, \ldots, y_{t^{\prime}-1}, c\right) $$
为了对这种序列中的条件概率建模,我们需要使用另一个RNN作为解码器。在输出序列中的任意时间步$t'$上,RNN接受之前时间步的输出$y_{t'-1}$以及上下文变量$c$作为输入,并且将它们以及之前时间步的隐藏状态$s_{t'-1}$一起变换为当前时间步的隐藏状态$s_{t'}$。
使用上述输入,解码器将获得当前时间步t的隐藏状态$s^{t^′}$。若使用函数$g$表达解码器隐藏层的变换,则有
$$ s_{t^{\prime}}=g\left(y_{t^{\prime}-1}, c, s_{t^{\prime}-1}\right). $$
有了解码器的各个时间步上的隐藏状态后,我们可以使⽤输出层和softmax运算来计算条件概率$P\left(y_{t^{\prime}} \mid y_{1}, \ldots, y_{t^{\prime}-1}, c\right)$。
训练模型
根据最⼤似然估计,我们可以最⼤化输出序列基于输⼊序列的条件概率:
$$
\begin{aligned}
P\left(y^{1}, \ldots, y^{t^{\prime}-1} \mid x^{1}, \ldots, x^{T}\right)
&=\prod_{t^{\prime}=1}^{T^{\prime}} P\left(y^{t^{\prime}} \mid y^{1}, \ldots, y^{t^{\prime}-1}, x^{1}, \ldots, x^{T}\right)
&=\prod_{t^{\prime}=1}^{T^{\prime}} P\left(y^{t^{\prime}} \mid y^{1}, \ldots, y^{t^{\prime}-1}, C\right).
\end{aligned}
$$
并得到该输出序列的损失:
$$ -\log P\left(y^{1}, \ldots, y^{t^{\prime}-1} \mid x^{1}, \ldots, x^{T}\right)=-\sum_{t^{\prime}=1}^{T^{\prime}} \log P\left(y^{t^{\prime}} \mid y^{1}, \ldots, y^{t^{\prime}-1}, C\right). $$
评估预测的序列
通过将预测序列与标签序列(the ground-truth)对比进行衡量。双语替换评测(英语:bilingual evaluation understudy,缩写:BLEU)是用于评估自然语言的字句用机器翻译出来的品质的一种算法。BLEU最早由Papineni et al., 2002提出用于评估机器翻译的结果,然而其在其他应用上也广泛使用。原则上,对于预测序列中的任意n-grams,BLEU可以评估这个n-grams是否出现在标签序列(label sequence)中。
n-grams的精度(precision)使用$p_n$表示,其代表着预测序列和标签序列中匹配的n-grams的数量与预测序列中的总n-grams数量的比值。为了更好解释,给定一个标签序列A,B,C,D,E,F,以及预测序列A,B,B,C,D,我们可以记错$p_1=4/5$(n-grams中$n=1$时),$p_2=3/4$(A-B、B-C、C-D),$p_3=1/3$(B-C-D),$p_4=0$.
另外,令$l_{\text{label}}$和$l_{pred}$分别代表标签序列和预测序列中的单词数。于是,BLEU可以定义为: $$ \left(\min\left(0, 1 - \frac{l_{\text{label}}}{l_{\text{pred}}}\right)\right) \prod_{n=1}^k p_n^{1/2^n} $$
其中$k$表示匹配最长的n-grams的n。基于BLEU的定义式,当预测序列与标签序列完全一致时,BLEU的值为1。此外,由于越长的n-grams越难成功匹配,为了对其精度值进行调整,BLEU会对越长的n-grams的精度赋予越大的权重。特别地,当$p_n$是固定的时候,$p_n^{1/2^n}$会随着n的增加而增大(初始论文中使用的是$p_n^{1/n}$)。
由于预测越短的序列,得到的$p_n$值也就会越高,在BLUE定义式中的前面的指数项其实就是对短序列的一种惩罚项。例如,当$k=2$时,给定标签序列$A,B,C,D,E,F$以及预测序列$A,B$,尽管$p_1=p_2=1$,而惩罚项因子$\exp(1-6/2)\approx 0.14$会将整个BLEU得分降低。