文本分类
简介
文本分类是一个非常流行的任务。例如在你在使用邮件系统时,就享受到了文本分类器的便利:正常邮件与垃圾邮件分类。其他应用还包括文档分类(document classification)、评论分类(review classification)等。
◎ 文本分类任务
文本分类通常不是作为一个单独的任务,而是一个更大的任务流程中的一部分。例如,语音助手对你的话语进行分类,以了解你想要完成的动作(如设置闹钟、叫一个出租车或者就是与语音助手聊天),根据语音助手中的分类器的决策,将这些信息传递给不同模型来完成相应动作。另一个例子是网络搜索引擎:它可以使用分类器来识别查询语言来预测你查询的类型,例如信息、导航、交易等。
因为大多数的分类数据集都假设一个数据只有一个对应正确标签,即单标签分类(single-label classification)。此外,也存在多标签分类问题(multi-label classification)。
分类数据集
用于文本分类的数据集在大小(数据集大小和示例大小)、分类内容和标签数量方面都存在很大差异。下图显示了一些文本分类数据集的统计差异:
| 数据集 | 类型 | 标签数量 | (训练集/测试集)大小 | 每个token的平均长度 |
|---|---|---|---|---|
| SST | 情感 | 5 or 2 | 8.5k / 1.1k | 19 |
| IMDB 影评 | 情感 | 2 | 25k / 25k | 271 |
| Yelp 评价 | 情感 | 5 or 2 | 650k / 50k | 179 |
| Amazon 评价 | 情感 | 5 or 2 | 3m / 650k | 79 |
| TREC | 问题 | 6 | 5.5k / 0.5k | 10 |
| Yahoo! Answers | 问题 | 10 | 1.4m / 60k | 131 |
| AG's 新闻 | 主题 | 4 | 120k / 7.6k | 44 |
| Sogou 新闻 | 主题 | 6 | 54k / 6k | 737 |
| DBPedia | 主题 | 14 | 560k / 70k | 67 |
其中最流行的数据集是情感分类(sentiment classification)数据集。这样的数据由电影评论、景点评论、饭店评论、产品评论等组成。此外,也存在一些问题分类数据集和主题分类数据集。
为了更好理解典型的分类任务,我们以SST数据集的描述为例。
- SST: 一个情感分类数据集,由电影评论组成
- 该数据集由句子的分析树组成,不仅是整个句子,较小的短语也都有对应的情感标签。
- 一个有5个标签:1(非常消极),2(消极),3(中性),4(积极),5(非常积极)
- SST存在一个二分类的变种数据集——SST-2,其中标签只有积极和消极两种
- SST一共包含215,154个短语,这些短语将组成各个影评
- Makes even the claustrophobic on-board quarters seem fun.

总览
假设我们有一个带有真实标签(ground-truth)的文档集合。一个分类器的输入是一个文档$x=(x_1, \dots, x_n)$,其中$(x_1, \dots, x_n)$是tokens,输出是标签$y\in 1\dots k$.通常。一个分类器会估计所有类别的概率分布,并且以概率值最高的类别作为预测输出。
获取特征表示并分类
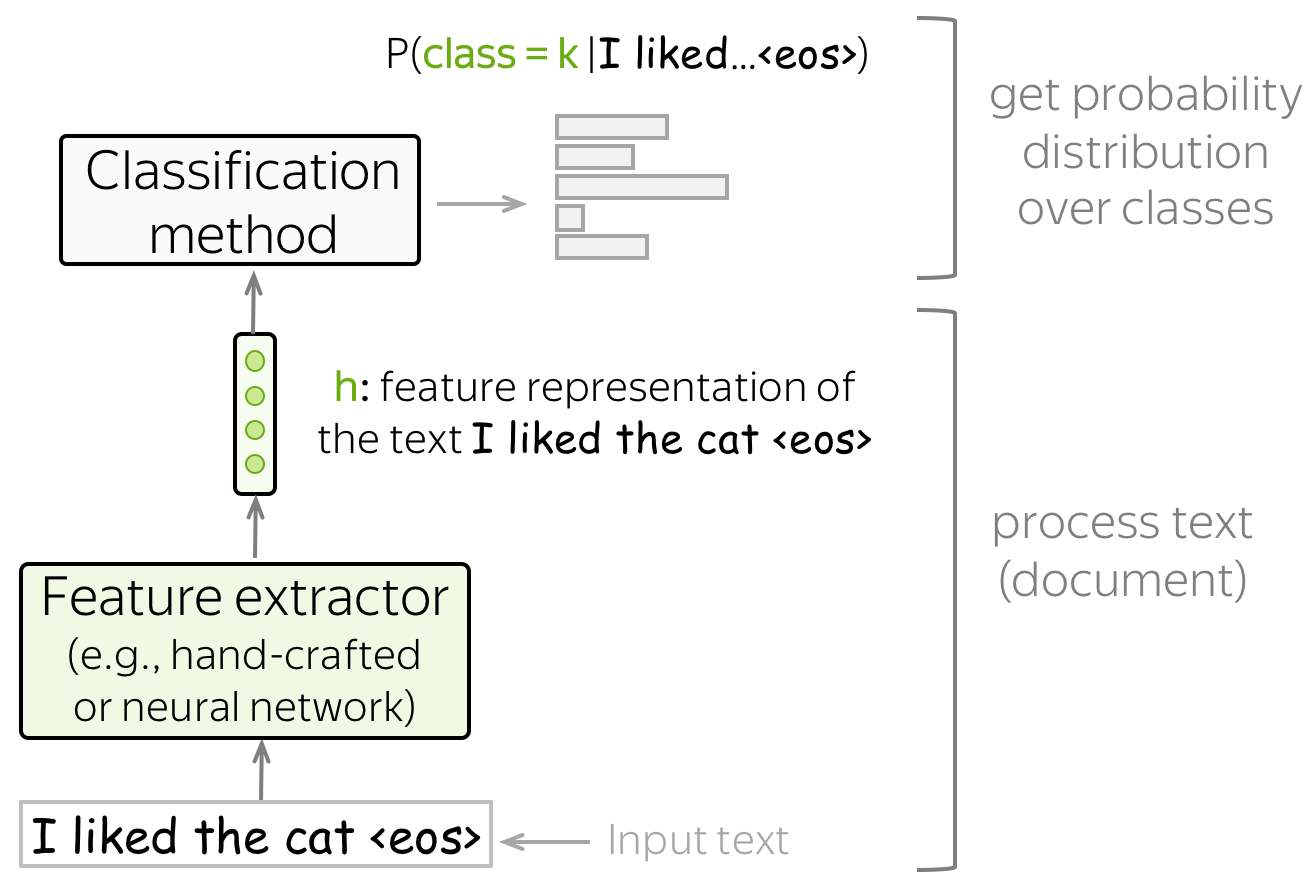
文本分类器有如下结构:
- 特征提取器 feature extractor
一个特征提取器要么被手动定义(例如传统的机器学习方法),要么可以自动学习得到(例如基于神经网络的方法)。
- 分类器
给定文本的特征表示,一个分类器需要给标签赋予概率值。最常见的方法是通过逻辑回归获得概率值。当然也存在其他变形,例如朴素贝叶斯分类器或者SVM。
生成模型和判别模型
 ◎ 生成模型与判别模型区别
◎ 生成模型与判别模型区别
一个分类模型要么是生成模型(generative)要么是判别模型(discriminative)。
- 生成模型
生成模型学习数据的联合分布$p(x, y) = p(x|y)\cdot p(y)$。为了根据输入$x$获得一个预测,生成模型将以联合概率最高的类别作为预测: $$ y = \arg \max\limits_{k}p(x|y=k)\cdot p(y=k) $$
- 判别模型
判别模型只对条件概率$p(y|x)$感兴趣,即它们只学习类别间的边界。为了根据给定输入$x$进行预测,判别模型将以条件概率最大的类别作为预测: $$ y = \arg \max\limits_{k}p(y=k|x) $$
文本分类的传统方法
朴素贝叶斯分类器Naive-Bayes-Classifier
原理
朴素贝叶斯方法的高层次思想是:根据贝叶斯定理,给出类别的条件概率另一形式,并且最终归结为计算$P(x|y=k)\cdot P(y=k)$

由于朴素贝叶斯方法通过对数据的联合分布建模,因此朴素贝叶斯方法是一个生成模型,
 ◎ 朴素贝叶斯模型的思想
◎ 朴素贝叶斯模型的思想
我们对使用到的术语进行如下描述:
- 先验概率$P(y=k)$: 在浏览观测数据之前(即在得到$x$之前),经验式的类别概率
- 后验概率$P(y=k|x)$(posterior): 在浏览观测数据之后(即在得知具体的$x$值后)的类别概率
- 联合概率$P(x,y)$: 数据的联合概率,即样本$x$和标签$y$
- 最大后验估计(Maximum a posteriori estimate, MAP): 选取后验概率最高的类别作为估计
如何定义$P(x|y=k)$和$P(y=k)$
- $P(y=k)$: 通过计算标签出现的频数
$P(y=k)$非常容易计算:我们只需要计算标签$k$在文档中出现的频率(这个是最大似然估计MLE的结果),即: $$ P(y=k)=\frac{N(y=k)}{\sum\limits_{i}N(y=i)}, $$
其中$N(y=k)$是文档中标签为$k$的样本数。
- $P(x|y=k)$: 使用“朴素”假设,再计数、
首先,我们假设文档$x$由一组特征表示,例如一组单词$(x_1, \dots, x_n)$,则有: $$ P(x| y=k)=P(x_1, \dots, x_n|y). $$
朴素贝叶斯假设为:
- 词袋假设(Bag of words assumption): 单词的顺序不重要
- 条件独立假设: 给定类别,特征(单词)之间是相互独立的
直觉上,我们假设标签为$k$的词在文档中出现的概率不取决于其所在的上下文,也不取决于单词顺序和其他的单词。例如,我们可以说awesome,brilliant,great更容易出现在积极情感的文档中;awful,boring,bad更容易出现在消极情感的文档中,但是我们却不知道这些词会怎么影响到其他的单词。
有了这些朴素假设,我们可以得到$P(x|y=k)$的计算式: $$ P(x| y=k)=P(x_1, \dots, x_n|y)=\prod\limits_{t=1}^nP(x_t|y=k). $$
概率$P(x_i|y=k)$由单词$x_i$在$k$类文档中的所有单词中出现频数为估计:
$$
P(x_i|y=k)=\frac{N(x_i, y=k)}{\sum\limits_{t=1}^{|V|}N(x_t, y=k)},
$$
其中如果$N(x_i, y=k)=0$,即在训练中,在$k$类文档中并没有出现$x_i$,那么整个$P(x|y=k)$的值都将会归零,这显然不是我们想要的。
 ◎ 部分词未在文档中出现时
例如, 在训练集的积极样本中,一些罕见的词,如pterodactyl或abracadabra没有出现,但这并不代表这些词不可能包含在一个积极情感的文档中。
◎ 部分词未在文档中出现时
例如, 在训练集的积极样本中,一些罕见的词,如pterodactyl或abracadabra没有出现,但这并不代表这些词不可能包含在一个积极情感的文档中。
为了避免这个情况,我们可以使用到一个简单的技巧:对所有词的计数结果都加上一个很小的平滑值$\delta$: $$ P(x_i|y=k)=\frac{\color{red}{\delta} +\color{black} N(x_i, y=k) }{\sum\limits_{t=1}^{|V|}(\color{red}{\delta} +\color{black}N(x_t, y=k))} = \frac{\color{red}{\delta} +\color{black} N(x_i, y=k) }{\color{red}{\delta\cdot |V|}\color{black} + \sum\limits_{t=1}^{|V|}\color{black}N(x_t, y=k)} , $$
其中$\delta$值可以使用交叉验证获取。
当$\delta=1$时,上式平滑方式就是拉普拉斯平滑(Laplace smoothing)。
进行预测
在上述内容中提到,朴素贝叶斯(或者更广泛一点:生成模型)是基于数据和类别间的联合分布做出预测: $$ y^{\ast} = \arg \max\limits_{k}P(x, y=k) = \arg \max\limits_{k} P(y=k)\cdot P(x|y=k). $$
直觉上,朴素贝叶斯期待一些词能够成为类别指示器(class indicators)。例如,在情感分类中,如果给定文本类别是积极情感,则像awesome,
brilliant, great这一类词通常会比在消极文本中有更高的概率,即$P( \mathrm{awesome} \mid {\color{#88bd33}{y=+}}) \gg P( awesome \mid {\color{red}{y=-}})$。

额外笔记
- 实践技巧: 使用对数概率和而不是概率乘积。
Sum of Log-Probabilities Instead of Product of Probabilities.
朴素贝叶斯用于分类的主要表达式是概率乘积: $$ P(x, y=k)=P(y=k)\cdot P(x_1, \dots, x_n|y)=P(y=k)\cdot \prod\limits_{t=1}^nP(x_t|y=k). $$
然而,许多概率的乘积可能会导致数值不稳定,因此,通常我们不使用$P(x,y)$,而是使用$\log P(x,y)$: $$ \log P(x, y=k)=\log P(y=k) + \sum\limits_{t=1}^n\log P(x_t|y=k). $$ 由于我们的目的是求$\arg\max$,因此将$P(x,y)$替换我$\log P(x,y)$并不会影响分类结果。
- 通用框架
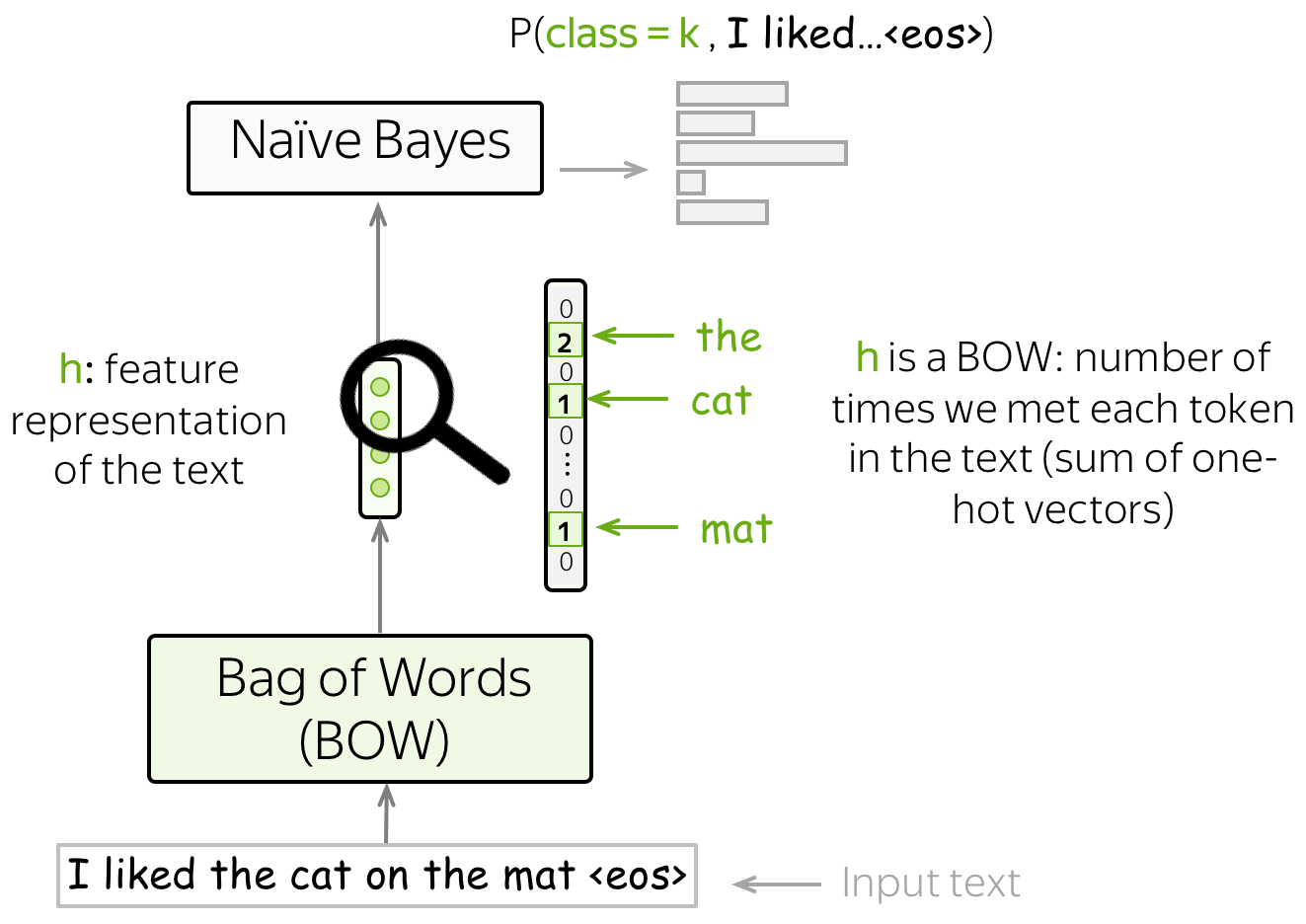
在朴素贝叶斯中,我们的特征是单词,以及特征表示为词袋(Bag-of-Words, BOW)表示——单词的独热编码的累加和。事实上,为了估计$P(x,y)$,我们只需要计算每个单词在文档中出现的频数即可。
- 特征设计
在标准的设计中,我们将单词作为特征输入。然而,我们也可以使用其他类型的特征,例如网站地址(URL)、用户ID等。
最大熵分类器-aka-逻辑回归
原理
与朴素贝叶斯算法不同,MaxEnt分类器(Maximum Entropy)是一个判别模型,即我们的关注点在于$P(y=k|x)$而不是联合分布$P(x,y)$。同时,在MaxEnt模型中,我们需要学习如何使用特征,而朴素贝叶斯是需要我们自定义使用特征的方法。
MaxEnt分类器同样需要我们手动定义特征,但是自由度更高:特征不需要一定是分类类型(categorical),而在朴素贝叶斯中,数据必须为分类类型。我们可以使用BOW表示或者使用一些更有意思的特征表示方法。
一个寻常的分类流程为:
-
获取输入文本的特征表示: $\color{#7aab00}{h}\color{black}=(\color{#7aab00}{f_1}\color{black},\color{#7aab00}{f_2}\color{black}, \dots, \color{#7aab00}{f_n}\color{black}{)}$
-
获取每个类别的特征权重向量: $w^{(i)}=(w_1^{(i)}, \dots, w_n^{(i)})$, 一个类别对应一个权重向量
-
对每个类别,将特征进行加权,即将特征表示$\color{#7aab00}{h}$与特征权重向量$w^{(k)}$做点积: $w^{(k)}\color{#7aab00}{h}\color{black} =w_1^{(k)}\cdot\color{#7aab00}{f_1}\color{black}+\dots+w_n^{(k)}\cdot\color{#7aab00}{f_n}\color{black}{, \ \ \ \ \ k=1, \dots, K.}$
- 为了在上述累加和中加入偏置项,我们定义一个值为1的特征$\color{#7aab00}{f_0}=1$,则有$w^{(k)}\color{#7aab00}{h}\color{black} = \color{red}{w_0^{(k)}}\color{black} + w_1^{(k)}\cdot\color{#7aab00}{f_1}\color{black}+\dots+ w_n^{(k)}\cdot\color{#7aab00}{f_{n}}\color{black}{, \ \ \ \ \ k=1, \dots, K.}$
-
使用softmax函数获得每个类别的概率:
$$ P(class=k|\color{#7aab00}{h}\color{black})= \frac{\exp(w^{(k)}\color{#7aab00}{h}\color{black})}{\sum\limits_{i=1}^K \exp(w^{(i)}\color{#7aab00}{h}\color{black})}. $$
Softmax将在上一步中做点积获得的$K$个值归一化为输出类上的概率分布。
 ◎ 每个类别的权重向量$w_k$与文本的特征表示$h$做点积
◎ 每个类别的权重向量$w_k$与文本的特征表示$h$做点积
训练:极大似然估计
给定训练样本$x^1, \dots, x^N$以及对应的标签$y^1, \dots, y^N$,其中$y^i\in{1, \dots, K}$。我们需要优化的是每个类别对应的特征选择向量$w^{(k)}, k=1..K$。通过在训练集数据中最大化如下概率,获得$w^{(k)}$的最优解: $$ w^{\ast}=\arg \max\limits_{w}\sum\limits_{i=1}^N\log P(y=y^i|x^i). $$ 换句话说,我们选择参数使得数据${x^i,y^i}_{i=1}^N$出现的概率最大。因此,这个训练目标也称为参数的极大似然估计(maximum likelihood estimate, MLE)。
为了寻找使得数据的对数似然函数值最大的参数,我们使用梯度下降算法进行优化:通过多次对数据迭代更新,逐步改进权重向量$w$。最终,给定样本$x^i$,获得正确标签$y^i$的概率值最大。
等价于最小化交叉熵: 最大化数据的对数似然,其实等价于最小化目标标签的概率分布 $p^{\ast} = (0, \dots, 0, 1, 0, \dots)$(1表示目标标签,0表示其他标签) 与模型预测的标签分布 $p=(p_1, \dots, p_K), p_i=p(i|x)$之间的交叉熵函数:
因为$p^{\ast}$中只有一个$p_i^{\ast}$不为0,即目标标签$k$为1,其余标签为0,我们可以将上式简化:
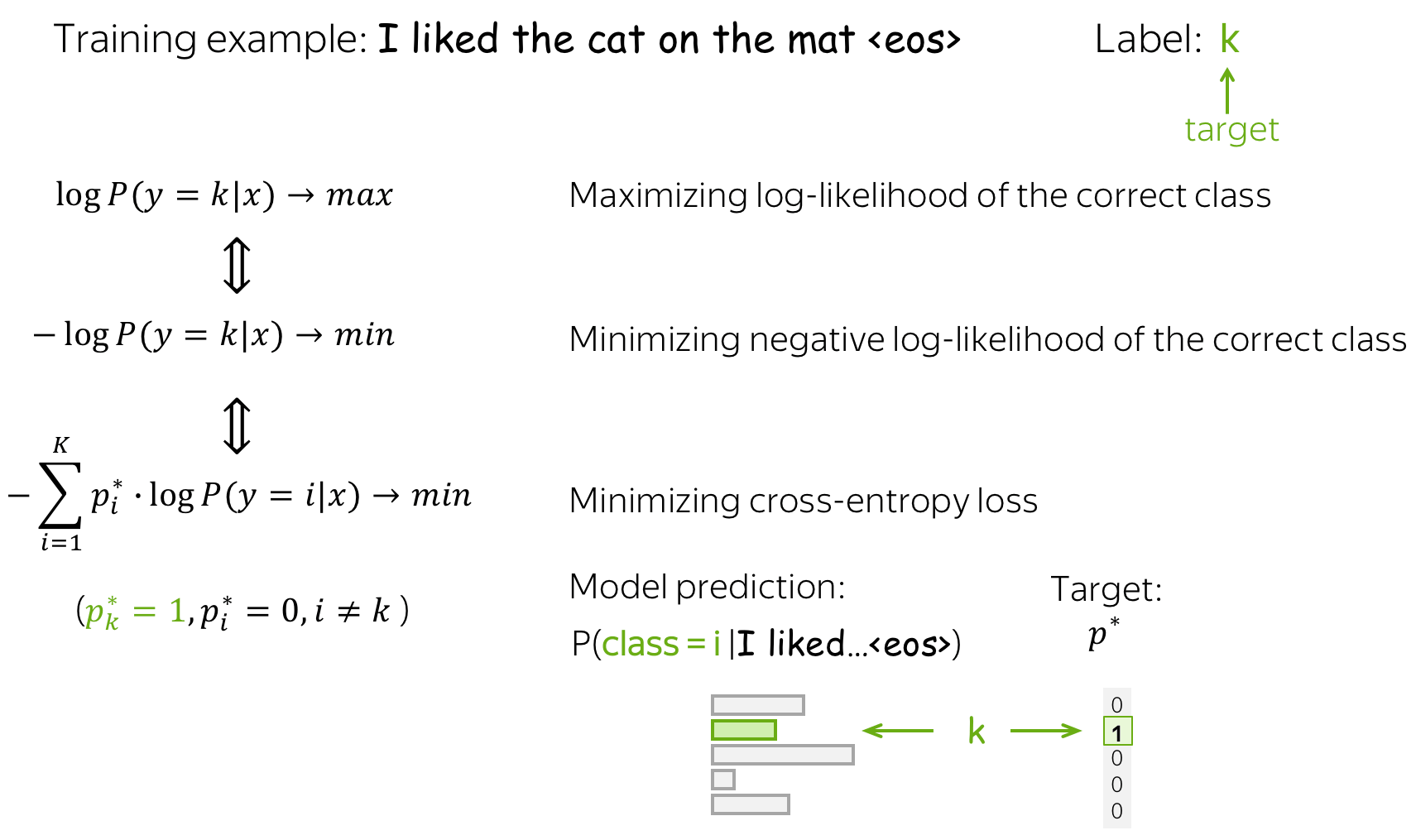
这种等价性对于理解逻辑回归很重要:当使用神经网络的方法时,通常会采用最小化交叉熵损失的方法优化。不要忘记其实这也与最大化数据的对数似然是等价的。
朴素贝叶斯 vs 逻辑回归
最后,对比两个方法的优缺点。

- 简洁性:
- 两个方法都非常简单,而朴素贝叶斯要更加简单一点
- 可解释性:
- 两个方法都具有较好的解释性,可以清楚知道哪些特征(词)对文本的分类具有影响
- 训练速度:
- 朴素贝叶斯的训练速度非常快,只需要将训练数据前馈一次用于统计频数,即可获得预测
- 逻辑回归需要多次梯度下降更新才能收敛
- 独立性假设:
- 朴素贝叶斯是真的很“朴素”,因为它假设了给定类别,特征(词)之间是相互独立的
- 逻辑回归不需要这样的假设
- 文本表示: 手动 manual
- 两个方法都需要手动定义特征表示,在朴素贝叶斯中,通常使用BOW作为标准选择,但也可以自己设定
- 有时,一种定义特征的方法可能对于模型的解释性有帮助,然而却可能降低模型预测性能
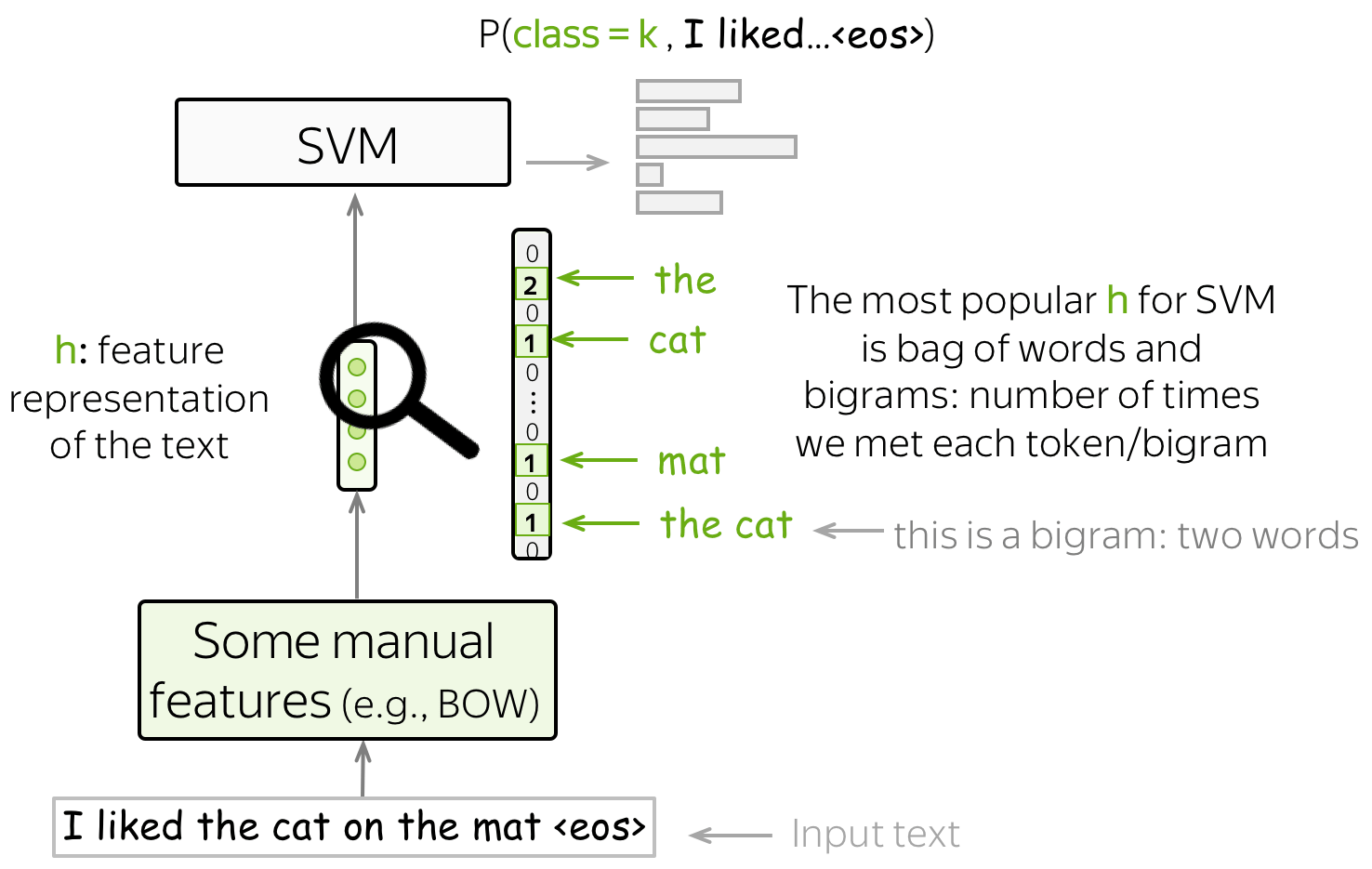
使用SVM做文本分类
使用SVM做文本分类时,也需要手动定义特征。最基本也是最流行定义特征的方式是BOW和Bag-of-ngrams(n-grams是n个词组成的元组)。有了这些简单的特征,使用线性核函数的SVMs就比朴素贝叶斯的分类性能要更佳。
基于神经网络的文本分类
原理
基于神经网络的文本分类的主要思想:通过使用神经网络,可以自动获得输入文本的特征表示。我们将输入tokens的嵌入表示传给神经网络,然后该网络会返回给我们输入文本的向量表示。
 ◎ 传统分类方法与神经网络方法对比
◎ 传统分类方法与神经网络方法对比
当处理神经网络时,我们可以使用一种简单的方式考虑分类部分(即如何从文本的向量表示中获得类别的概率)。
文本的向量表示假设有$d$维,但最后我们只需要一个$K$维的向量来表示各个类别的概率。为了从一个$d$维向量中获得一个$K$维的向量,我们可以使用一个线性层。一旦我们有了$K$维向量,剩下只需要将该向量交给softmax函数,将该$K$维向量转换为各个类别的概率。
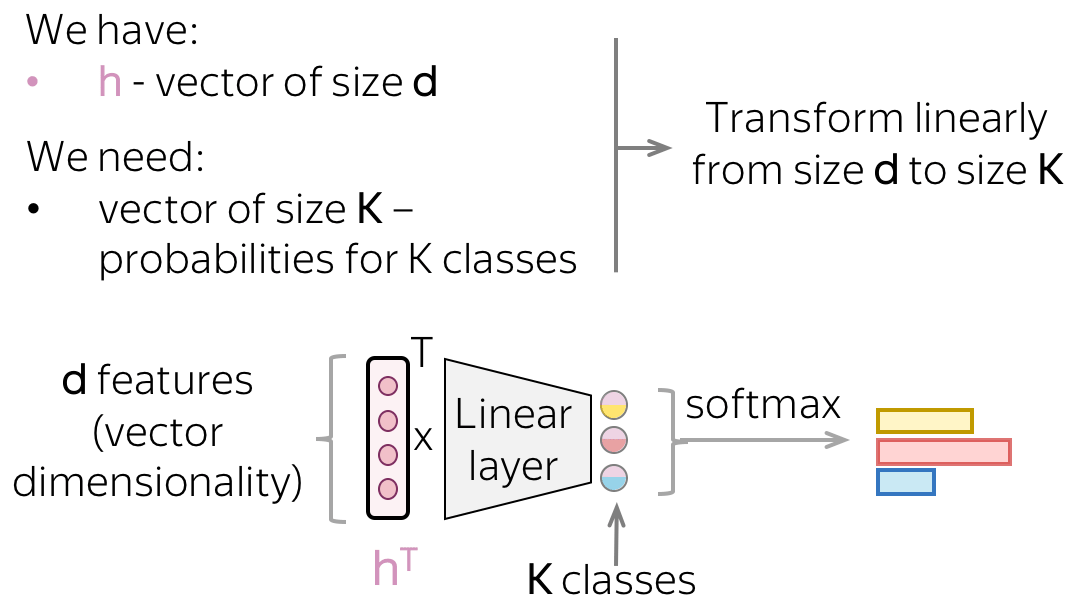
分类部分:这是一个逻辑回归
如果仔细观察神经网络分类器,我们处理输入文本的向量表示的方式与逻辑回归中的处理方式一致。我们根据每个类别的特征权重,对特征加权。而两者的唯一区别在于:特征的来源;要么是手动定义的,要么通过网络获得。
 ◎ 逻辑回归的分类步骤与神经网络的分类步骤对比
◎ 逻辑回归的分类步骤与神经网络的分类步骤对比
直觉:文本表示(text representation)向量 $h$ 指向类表示(Class representation)向量 $w$ 的方向。

如果我们仔细观察最后的线性层,可以发现线性层权重矩阵的列元素即为向量$w_i$。这些向量可以被认为是类别的向量表示。一个好的神经网络将学会以这样的方式表示输入文本:文本向量将指向相应类向量的方向。
训练过程与交叉熵损失
神经网络分类器经过训练来预测各个类别的概率分布。直觉上,在每一步中,我们都将模型分配给正确类别的概率最大化。
标准的损失函数为交叉熵损失。对于目标概率分布$p^{\ast} = (0, \dots, 0, 1, 0, \dots)$(1代表目标标签,0表示其他标签)和由模型预测获得的概率分布$p=(p_1, \dots, p_K), p_i=p(i|x)$,两者的交叉熵损失函数为:
$$ Loss(p^{\ast}, p^{})= - p^{\ast} \log(p) = -\sum\limits_{i=1}^{K}p_i^{\ast} \log(p_i). $$
由于$p_i^{\ast}$中只有对应目标标签$k$的元素不为0 ,为1。因此,损失函数可以化简为$Loss(p^{\ast}, p) = -\log(p_{k})=-\log(p(k| x)).$

在训练中,我们通过对数据多次迭代更新,逐步改进模型的权重:我们对所有训练数据(或者批次训练数据)训练,并更新梯度。在每一步,我们将模型分配给正确类别的概率最大化。同时,我们也相等于最小化了错误类别的概率和:由于所有概率的总和为常数(1),通过增大其中一个概率,其他概率和就会随着减小。
回忆:最小化交叉熵损失函数等价于最大似然函数。
基于网络的文本分类模型
我们需要一个可以对不同长度的输入产生一个固定长度的向量。
在这个部分,我们将研究使用神经网络获取输入文本的向量表示的不同方法。注意到当输入文本可以有不同的长度,而文本的输出向量表示的大小是固定的,否则,网络将无法“工作”。

我们从仅使用词嵌入的最简单方法开始(不在其顶层添加模型),然后我们再研究循环和卷积神经网络。
基础:嵌入袋(BOE)和加权BOE
最简单的文本处理方法是仅使用单词嵌入,而不再其后增加任何神经网络。为了获得一段文本的向量表示,我们要么将所有的tokens的嵌入累加(Bag of Embeddings, BOE),或者使用这些嵌入的加权和(权重,可以是TF-IDF算法等)
嵌入袋(BOE)(最好搭配朴素贝叶斯)应该是任何具有神经网络的模型的基准(Baseline)。如果最终效果没有基准好,那么就不值得使用神经网络模型,不过这种情况可能是因为我们没有足够多的数据。

虽然有时嵌入袋(BOE)也被称为词袋(BOW),但请注意这两个概念是非常不同的。BOE是多个嵌入表示的累加和,而BOW是多个独热编码向量的累加和。BOE相比BOW,具有更多语言的信息。预训练的嵌入(例如Word2Vec,Glove)可以理解单词之间的相似性。例如,在BOE中,awesome,brilliant,great由相似的词向量表示,而在BOW中却使用毫无关联的特征表示。
此外,为了使用多个嵌入的加权和,我们需要想出一种获取权重的方法。然而,这恰恰是我们想要通过使用神经网络避免的事情:我们不希望加入手动定义的特征,而是使用神经网络去学习有用的模式(pattern)。
可以试试在BOE的基础上使用SVM算法。SVM与传统算法区分开的是核函数的选择:一般RBF核会更好。
循环网络模型(RNN/LSTM/etc)
原理
循环神经网络是一种非常自然地处理文本的方法,与人类相似,通过一个一个单词地阅读句子并处理这些信息,并可望网络的每一步都将“记住”它以前阅读过的所有内容。
- RNN 单元
在每个时间步上,一个RNN将接受一个新的输入向量(例如,token的嵌入)以及之前时间步RNN的隐藏状态(可望该隐藏状态可将之前所有的信息都编码进去)。通过使用这两个输入,RNN单元计算得到新的隐藏状态,并以此获得对应时间步的输出。这个新的隐藏状态包含着当前输入以及过去时间步输入的信息。
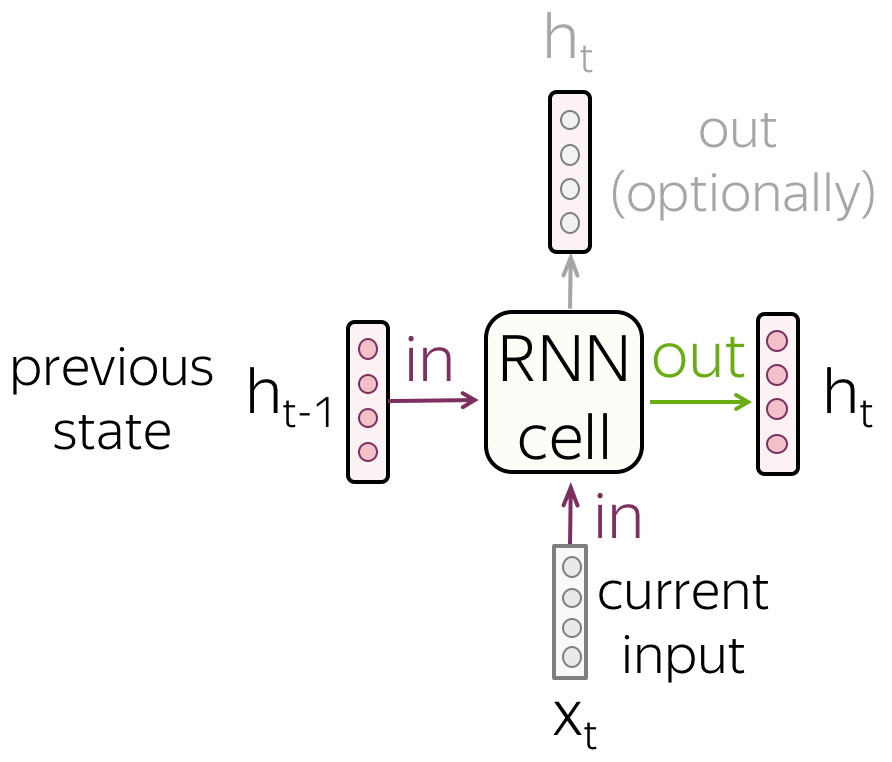
- RNN读取tokens组成的序列
RNN通过一个一个token的方式读取序列。在每个时间步上,RNN使用新读取token的嵌入和之前时间步的隐藏状态。
每个时间步上的RNN单元都是相同的。
- Vanilla RNN
最简单的RNN架构-Vanilla RNN,将之前时间步的隐藏状态$h_{t-1}$和当前时间步的输入数据$x_t$进行线性变换(矩阵乘积),然后再使用一个非线性激活函数转换(通常选择$\mathrm{tanh}$函数):
$$ h_t = \tanh(h_{t-1}W_h + x_tW_t). $$
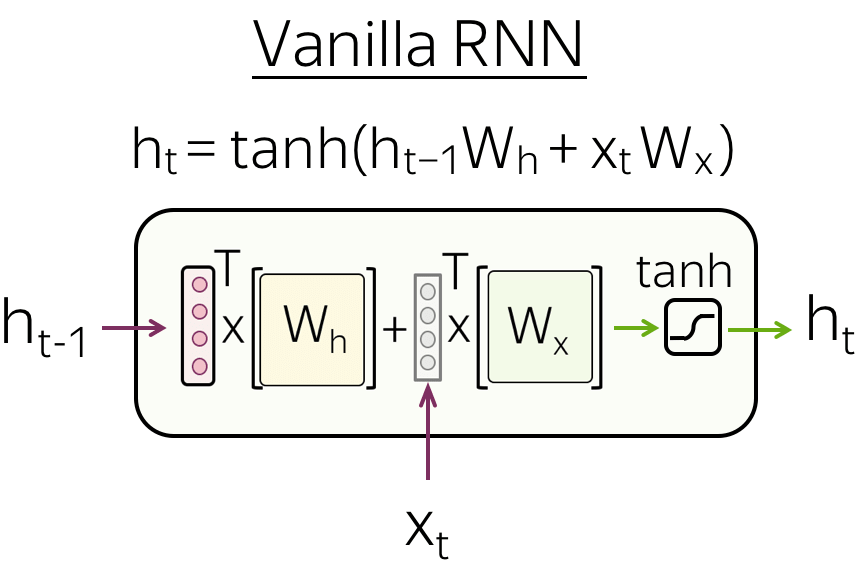
然而Vanilla RNN容易遭受梯度消失和梯度爆炸的问题。为了减缓这个问题,一些更复杂的循环网络单元被提出(如LSTM、GRU等)。
用于文本分类的循环神经网络
本小节将介绍循环网络是如何应用在文本分类任务中的。本节所有的循环网络通指"RNN"(如vanilla RNN, LSTM, GRU等)。
We need a model that can produce a fixed-sized vector for inputs of different lengths.
- 简单的RNN:读取文本,并进入最终状态
大多数简单的循环网络模型都是单层的RNN网络。在这种网络结构中,我们必须采用具有输入文本的大部分信息的隐藏状态。因此,我们必须使用最后一个时间步上的隐藏状态(因为最后一个时间步的隐藏状态将遍历了所有的输入tokens)。

- 多层结构:将一层RNN的隐藏状态传递给下一层RNN
为了获得更好的文本表示,我们可以叠加多层网络。例如下图中,高层的RNN输入来自之前层RNN输出的表示。
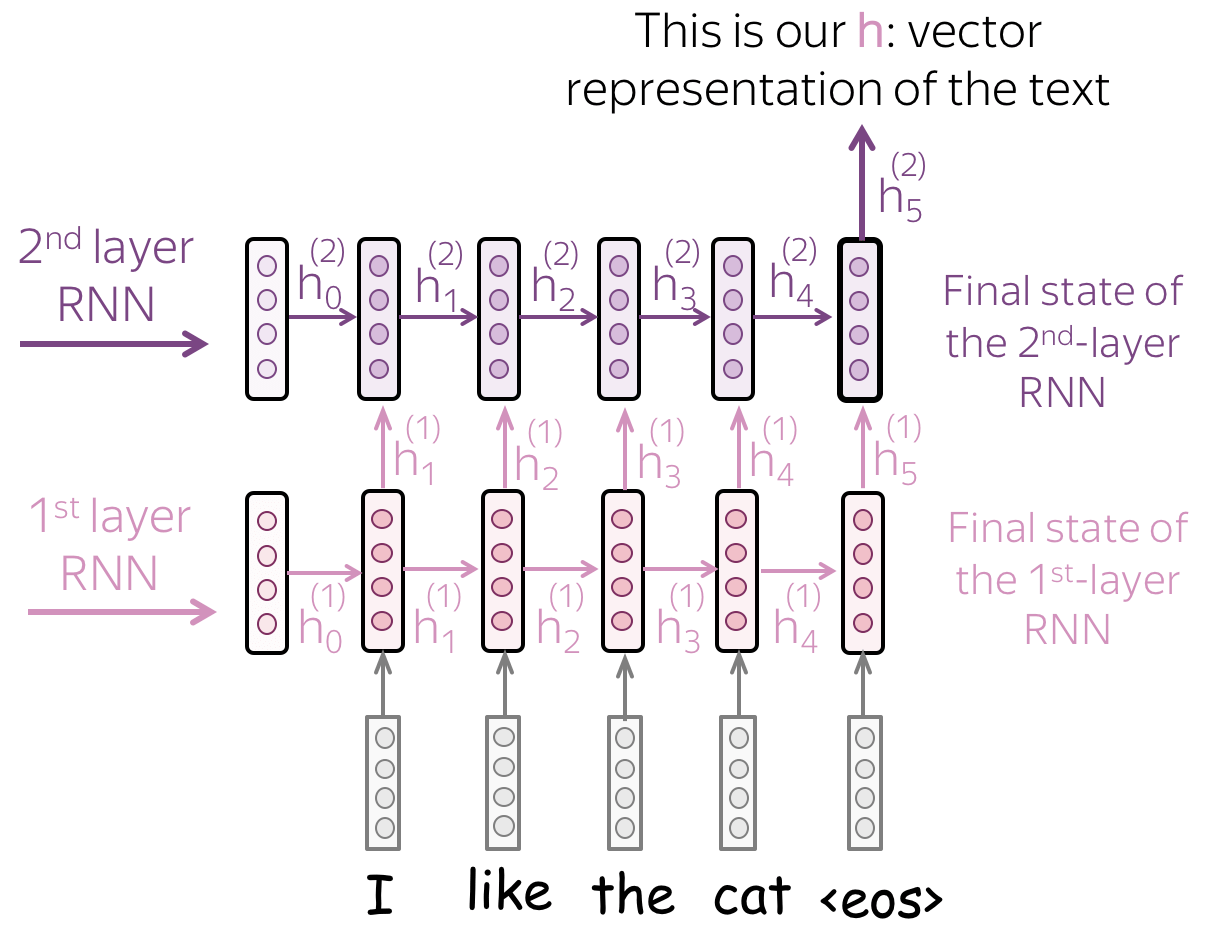
多层结构的主要假设是:有了多层网络,低层次的网络可以捕捉到文本的局部现象(例如,短语等),而高层次的网络可以学习到更高层次的信息(如文本主题)。
- 双向结构:使用前向和反向RNNs的最终状态
之前的循环网络结构都存在一个问题:最后时间步的隐藏状态很容易忘记之前的tokens信息,即使是非常强健的LSTM模型也会遭遇这个问题。
为了避免这个问题,我们可以使用两个RNNs:
- 前向(forward):从左到右读取输入
- 反向(backward): 从右到左读取输入
然后,我们可以使用两个循环网络结构的最终隐藏状态:一个网络会更好地记住文本的末尾部分,而另一个会更好地记住文本的开始部分。这些状态可以连接在一起,或者累加,或者做些别的操作。
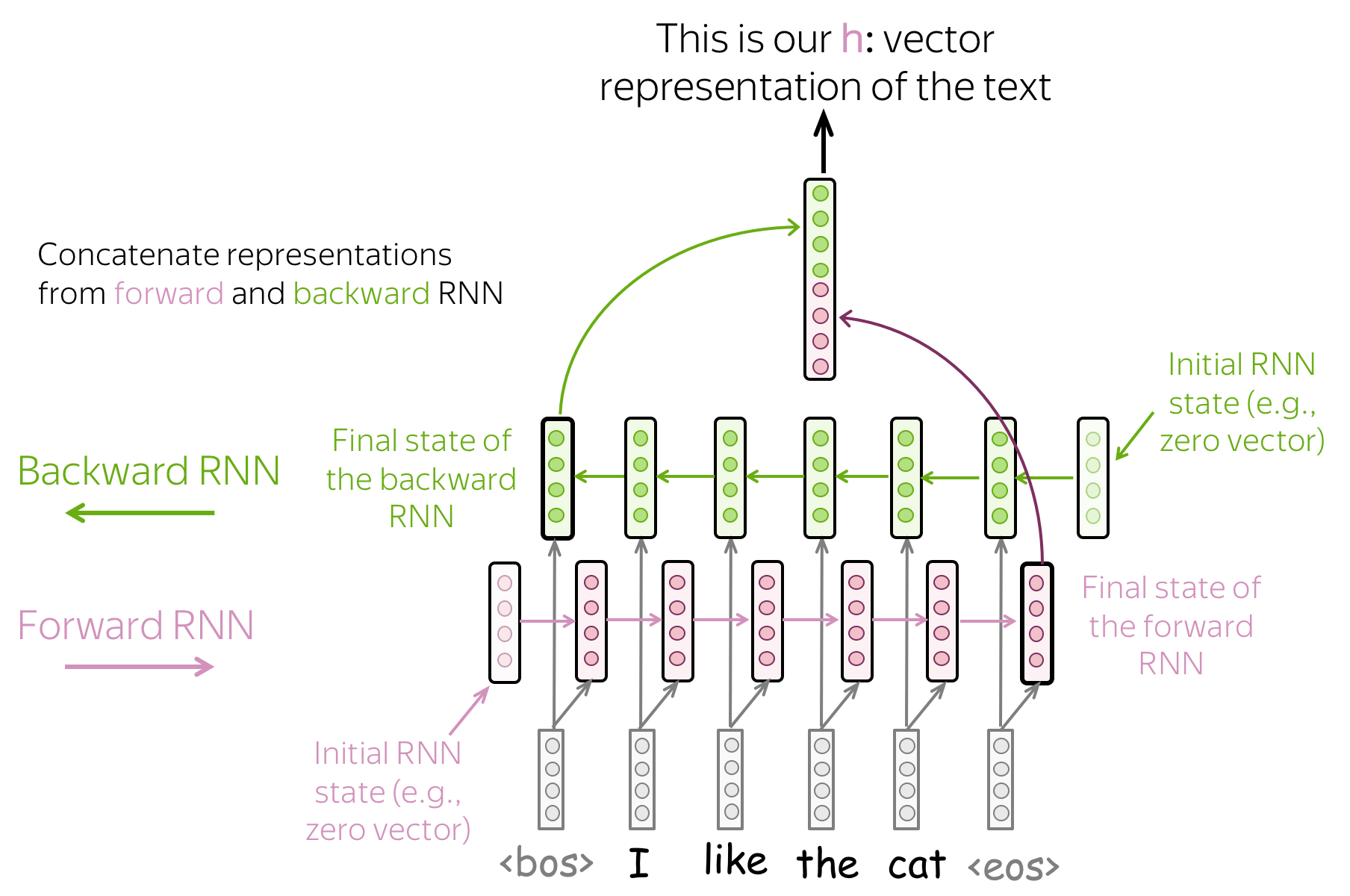
有了这些RNNs结构,我们就可以像搭积木一样,自由组合多种RNNs结构。
卷积神经网络(CNN)
图像卷积和平移不变性(Convolutions for Images and Translation Invariance)
卷积神经网络最初发明用于计算机视觉任务。因此,首先了解用于图像的卷积模型背后的直觉。
想象我们想要将图像分成多个类别,例如cat,dog,airplane等。在这个例子中,如果我们在图像中找到一只猫,我们不需要关系这只猫在图像的哪个位置,我们只需要关系猫是否在图像上。

卷积网络将相同的操作应用于图像的一小部分,这也是卷积网络如何提取特征的方式。每个操作都在寻找与模式匹配的内容,网络将学习到哪些模式有用。有了许多网络层,学习到的特征将会越来越复杂:从低层网络中学习到的线条特征到高层网络学习到的非常复杂的模式(如整只猫或狗)。
而卷积网络的这种特性被称为平移不变性(translation invariance):平移是因为我们讨论的是在空间的中移动,而不变形是因为我们想要的是空间中的移动对图像类别的识别没有影响。
将卷积用于文本的原理
对于图像,这个问题非常清楚,例如我们能够移动猫在图像上的位置,因为我们并不需要在乎猫在哪里。然而那文本呢?第一眼看,这个问题并不简单:我们不能轻易地移动文本中的短语——文本的含义会发生变化或者我们将获得一些说不通的语句。
然而,在某些应用中,我们可以想到相同的直觉。想象我们正在对文本进行分类,不是像图像一样分类cat,dog,而是分类为积极情感或消极情感。接着,文本中的一些单词和短语可能会具有非常多的信息暗示(cues)(例如It's been great, bored, absolutely amazing),而其他一些单词就不那么重要。也就是说,我们不需要太关心这些具有很大信息暗示的单词和短语在文本中出现的位置,就可以大概理解文本的情感!

一个经典的CNN模型:卷积+池化块
跟从上述想象中的直觉,我们想要识别出一些模式,但是我们并不需要对这些模式出现的位置过于关心。这样的行为可以通过两个网络层实现:
- 卷积层(convolution): 找到这些模式的匹配项
- 池化(pooling): 将这些匹配项汇总(要么局部汇总,要么全局汇总)
为了获得输入文本的向量表示,一个卷积网络通过一个非线性映射(通常是$\mathrm{ReLU}$)和一个池化操作,获得词嵌入。该获取表示,并用于分类的方式与其他网络是相似的。
 ◎ 用于文本分类的CNN架构
◎ 用于文本分类的CNN架构
用于文本的卷积层
卷积的想法是通过滑动窗口,遍历图像,并对每个窗口应用相同的操作,即卷积滤波器(convolution filter)。
用于图像的卷积是二维的,因为图像也是二维的(高和宽)。而与图像不同,文本只有一个维度,因此卷积操作也是一维的。
卷积是应用于每个输入窗口的线性层(紧随其后的是非线性变换)。
 ◎ 对文本的卷积操作
◎ 对文本的卷积操作
形式上,我们做出如下假设:
- $(x_1, \dots, x_n)$表示输入单词的表示,其中$x_i\in \mathbb{R}^d$
- $d$(输入通道):输入词嵌入的大小
- $k$(核的大小):卷积窗口的长度(在图示中是$k=3$)
- $m$(输出通道):卷积滤波器的数量

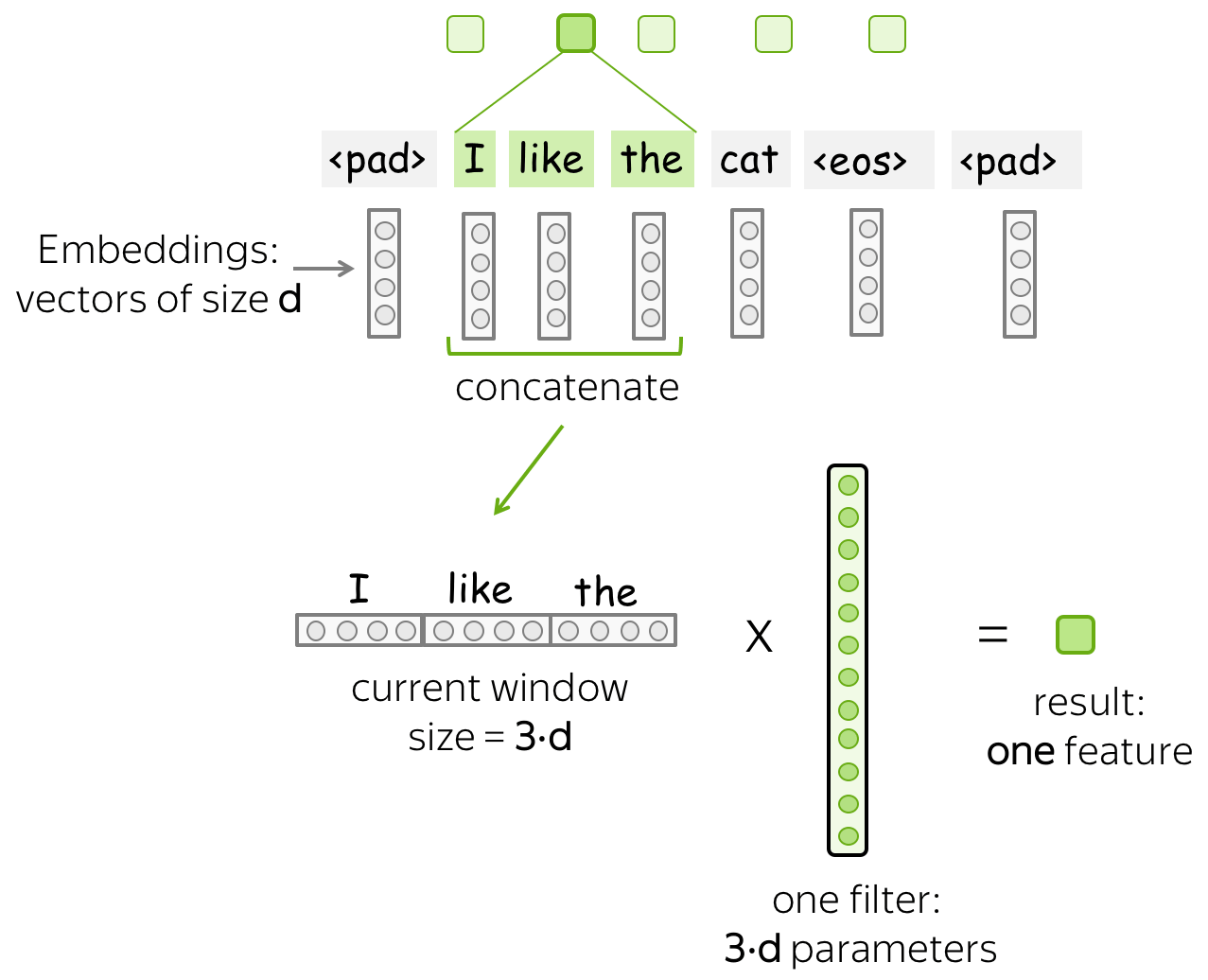
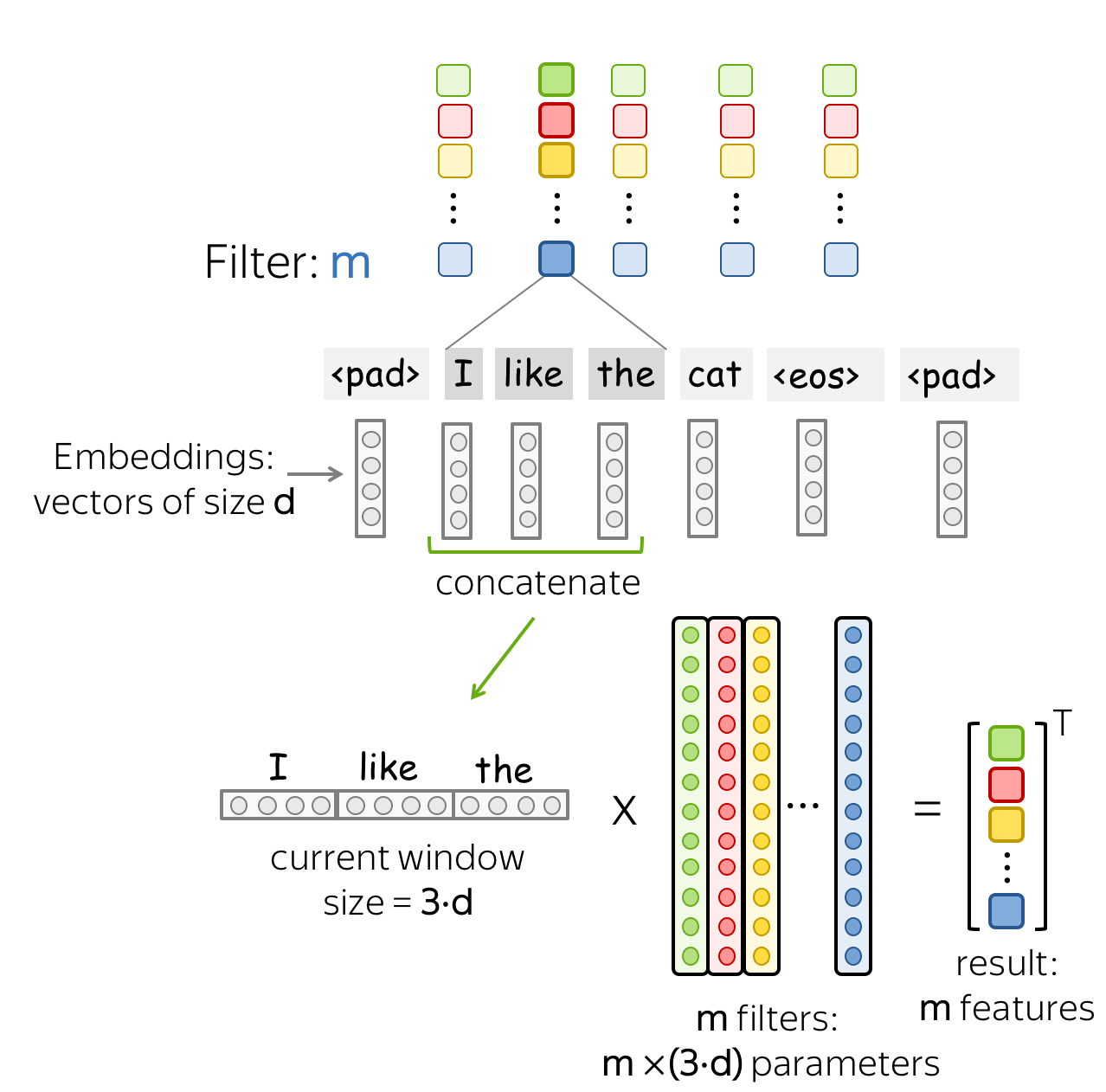
卷积层是一个线性变换层,其变换矩阵为$W\in\mathbb{R}^{(k\cdot d)\times m}$。对于一个大小为$k$的窗口$(x_i, \dots x_{i+k-1})$,卷积接受这些向量的连接( concatenation): $$ u_i = [x_i, \dots x_{i+k-1}]\in\mathbb{R}^{k\cdot d} $$ 然后与卷积矩阵相乘: $$ F_i = u_i \times W. $$ 卷积通过使用滑动窗口,遍历所有的输入,并对每个窗口应用相同的线性变换。
直觉:每个过滤器提取一个特征。
- 一个过滤器——一个特征提取器
一个过滤器采用当前窗口下的词表示,并将其线性转换成一个特征。形式上,对于窗口$u_i = [x_i, \dots x_{i+k-1}]\in\mathbb{R}^{k\cdot d}$,过滤器$f\in\mathbb{R}^{k\cdot d}$计算点积: $$ F_i^{(f)} = (f, u_i). $$
数值$F_i^{(f)}$(提取到的特征)是将过滤器$f$施加给窗口$(x_i, \dots x_{i+k-1})$的结果。
- $m$个过滤器——$m$个特征提取器
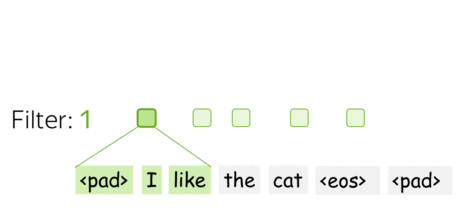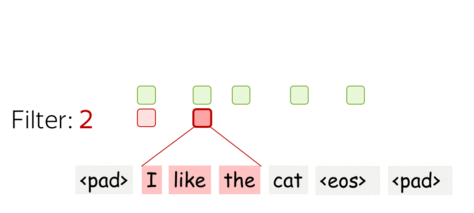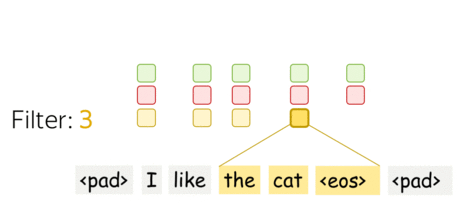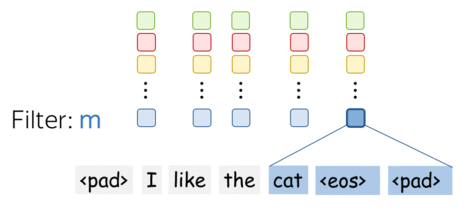
一个过滤器提取一种特征,那么我们使用多个过滤器即可提取多种特征。每个过滤器读取输入文本,并提到不同的特征。过滤器的数量是我们想要获得的输出特征的数量。有了$m$个过滤器,之前讨论的卷积矩阵大小将变为$(k\cdot d)\times m$。
这是并行完成的(parallel)!在上述图示中展示了CNN如何“读取”文本,而实际上这些计算是并行进行的。
池化操作
在卷积层从每个窗口提取到$m$个特征后,池化层将整合了某些区域的特征。池化层被用于降低输入维度,因此也可以降低网络使用的参数数量。
- 最大和平均池化(Max/Mean Pooling)
最流行的做法是最大池化:它将选取每个维度上的最大值,即选取每个特征的最大值输出。

平均池化与最大池化的工作原理相似,不过其操作是取每个特征的均值而不是最大值。
 ◎ k-max池化: 选取k个概率最高的值
◎ k-max池化: 选取k个概率最高的值
- 池化与全局池化(global pooling)
与卷积相似,池化也被用于几个元素组成的窗口中。池化还有一个步长(stride)参数,最常见的方法是对不重叠的窗口分别进行池化。为了做到这个操作,我们需要将步长设置为池化窗口大小一致。

池化与全局池化的差异在于池化将独立应用于每个窗口中的特征,而全局池化将对整个输入执行池化操作。全局池化通常被用于获取整个文本的单一向量表示;这种全局池化被称为max-over-time池化,其中“时间”轴从第一个输入token到最后一个token。

直觉上,每个特征在看到某种模式时都会“触发”,例如图像中的视觉模式(线条、纹理、猫爪等)或者一个文本模式(例如短语)。在池化操作后,我们将输出一个向量来说明有哪些模式存在于输入中。
使用CNN做文本分类
我们需要构建一个将文本表示为单个向量的卷积模型。
下图展示使用CNN做文本分类的基础模型框架:
 ◎ 文本分类CNN的基本框架
◎ 文本分类CNN的基本框架
在卷积操作后,我们采用的max-over-time的池化操作。这是一个非常关键的步骤:它将文本压缩为单个向量。模型本身可以有所不同,但是使用池化操作时,它必须使用全局池化来将整个输入文本压缩为单个向量。
Apply a max-over-time pooling to get a vector of fixed size.
- 几个使用不同大小核的卷积
除了使用只有一种大小核的卷积操作,我们还可以使用具有不同核大小的多个卷积。步骤很简单:对数据应用每个不同大小核的卷积,在每个卷积之后添加非线性和全局池化,然后合并结果(在图示中,为简单起见,省略了非线性)。
 ◎ 使用多种大小核的卷积,并最终连接成一个文本的向量表示
◎ 使用多种大小核的卷积,并最终连接成一个文本的向量表示
以上就是获取用于分类文本的向量表示的方式。
- 堆叠多个卷积+池化块
除了使用单个卷积-池化层,我们还可以卷积-池化层作为模块,叠加使用。在使用多个卷积-池化层模块后(可以使用一般的池化),我们可以叠加另一种卷积-池化层模块,而这一层池化需要使用到全局池化。
请记住:因为我们必须获得一个固定大小的向量,为此,需要使用全局池化。
当您的文本很长时,这种多层卷积可能会很有用。例如,如果当模型是字符级(character-level)的(而不是单词级word-level的)。
 ◎ 多层卷积+池化
◎ 多层卷积+池化
初始化的嵌入如何选择
Rand: 随机初始化嵌入矩阵Static: 采用word2vec预训练的嵌入,并且在训练网络过程中不对其更新Non-Static: 采用word2vec预训练的嵌入,并且在训练网络参数的同时,更新这些嵌入
多标签分类
简介
多标签分类(Multi-label classification)与之前讨论的单标签分类任务不同,多标签分类中每个输入都可以有多个正确的标签。例如,一条推特可以有多个标签(hashtags),一个用户可以有多种主题的兴趣等。
◎ 多标签任务举例
对于多标签问题,相较于单标签问题,我们需要改变以下两个内容:
- 模型:如何估计类别的概率
- 损失函数
模型:Softmax $\rightarrow$ 元素向Sigmoid
在最后的线性层之后,我们有$K$个类别对应的$K$个值,而我们需要将这些值转换为对应类别的概率。
在单标签问题中,我们使用softmax函数来做到这件事情,其将$K$个值转换为一个概率分布,即所有类别的概率和为1,而这意味着所有类别共享相同的概率密度。如果一个类别的概率很高,那么其他类别就不会有高的概率值。
而对于多标签问题,我们需要将这$K$个值转换为类别间相互独立的相应类别概率。具体来说,我们将对这$K$个值分别使用sigmoid函数 $\sigma(x)=\frac{1}{1+e^{-x}}$.
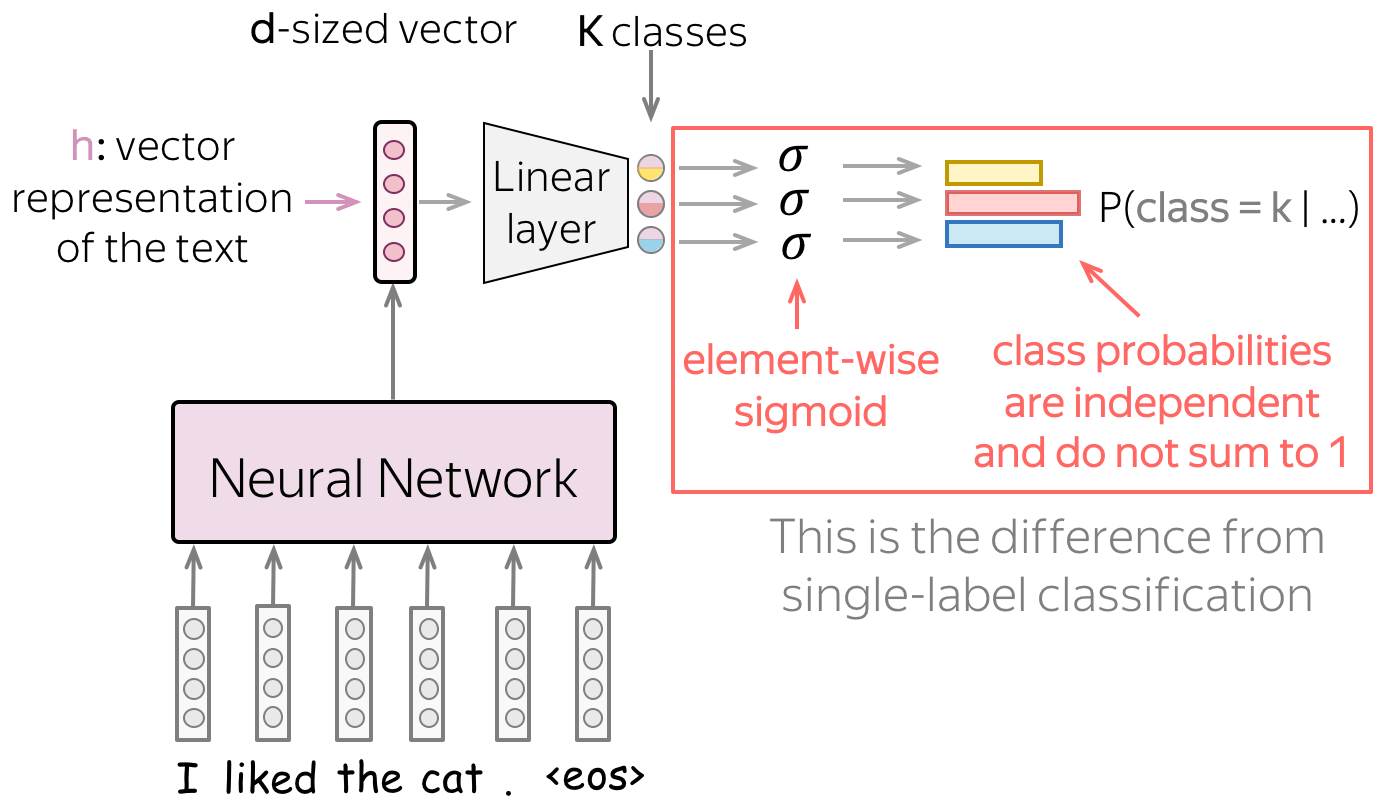
在直觉上,我们可以将多标签问题等价为$K$个独立的二分类问题。
损失函数:每个类别使用二值交叉熵
在多标签问题中,损失函数需要作出一定的改变来应用于多个标签:对每个类别,我们都使用二值交叉熵函数(binary cross-entropy loss)。
$$H_{p}(q)=-\frac{1}{N} \sum_{i=1}^{N} y_{i} \cdot \log \left(p\left(y_{i}\right)\right)+\left(1-y_{i}\right) \cdot \log \left(1-p\left(y_{i}\right)\right)$$

下图展示了二值交叉熵的直观推导流程[1]
◎ 二值交叉熵函数推导
实践技巧
词嵌入:如何处理?
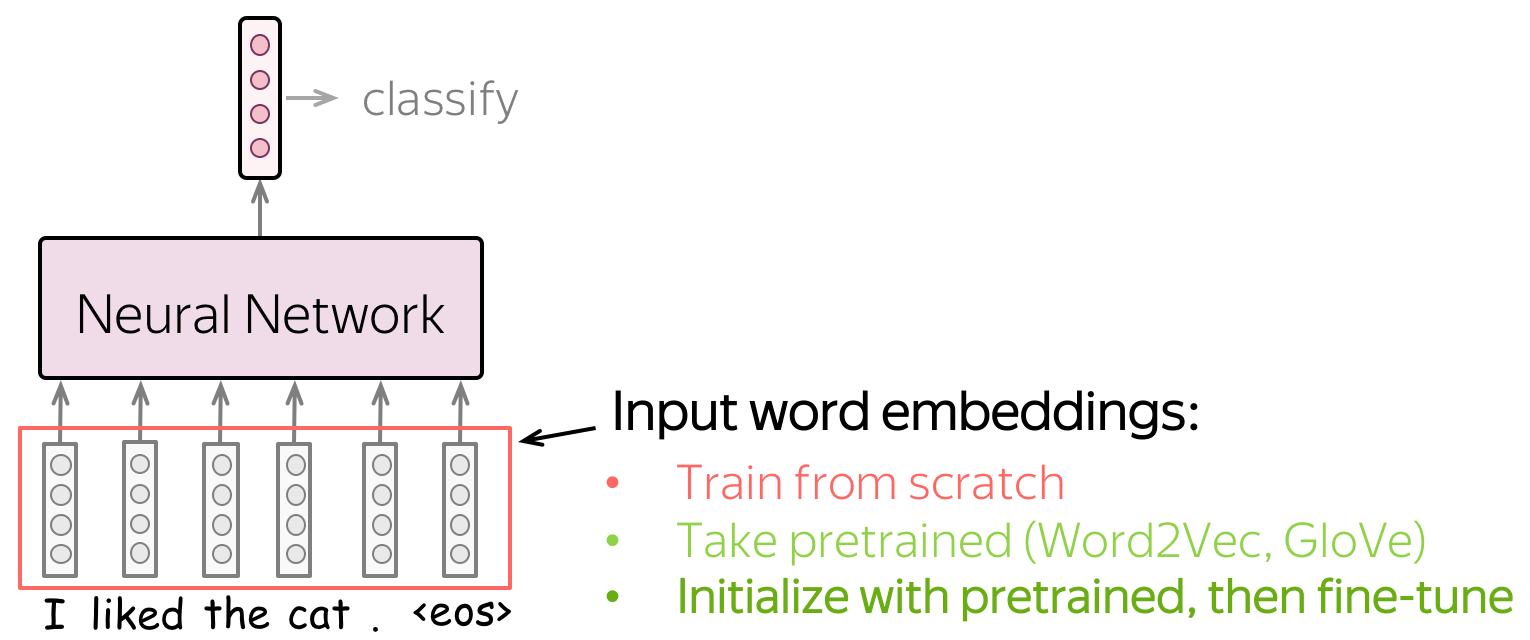
网络的输入由词嵌入表示,我们有三种选择获得这些词嵌入。
- 作为模型的一部分,从头开始训练
- 只使用特定任务的语料训练词嵌入
- 使用预训练的词嵌入(如Word2Vec,Glove等),并固定(将其作为静态向量使用)
- 使用预训练的词嵌入进行初始化,然后通过网络对其进行训练(“微调”)。
用于分类的训练数据是带有标记的,并且是与特定任务相应的,但是带有标记的数据通常很难获得。因此,这个语料库可能不会很大(至少),或者不会多样化,或者两者兼而有之。相反,词嵌入的训练数据是无需标记的,并且纯文本就足够了。因此,这些数据集可能庞大而多样,可以供网络学习很多东西。

现在,让我们根据对词嵌入的处理方式来考虑模型将学习的内容。
- 如果词嵌入是从头开始训练得到的,那么模型将会只“知道”分类数据,而不足够良好地学习单词之间的关系。
- 如果使用预训练的词嵌入,那么模型将知道一个很大的预料库,并且学习到很多内容
- 为了将这些词嵌入适用于我们手头特定的任务,我们可以通过整个网络训练这些预训练的词嵌入,对其进行微调。这样的做法可以使模型性能获得一定提升

当我们使用预训练的词嵌入时,其实就是迁移学习的一种体现:通过预训练的词嵌入,我们将预训练中的训练数据的知识“迁移”到我们特定的任务中。
那我们是否应该使用微调的预训练词嵌入呢?
在训练模型之前,可以首先考虑微调为什么会有用,以及哪些类型的任务可以从中受益,再做决定。
数据增强:“免费”获得更多的数据的方法
数据增强以不同的方式更改数据集,以获取同一训练数据集的“加强”版本。数据增强可以增加:
- 训练数据的数量
- 模型的质量很大程度上取决于样本的数量。对于深度学习模型,拥有大数据集至关重要
- 数据的多样性
- 通过提供不同版本的训练数据集,使模型对真实世界的数据更健壮(robust)
- 实践数据可能导致模型的性能降低,或者与训练数据略有不同。
- 使用增强数据集,模型不太可能适合特定类型的训练数据,而将更多地学习一般的模式。
图像的数据增强可以很容易地做到,一些标准的数据增强方式有:图像翻转(flipping),几何变换(例如旋转,在某个方向上拉长),用不同的色块覆盖图像的各个部分。

那么我们如何对文本做一样的事情呢?
- 单词丢弃(word dropout):最简单并且最流行的方式
单词丢弃是最简单的正则化方法:对每个样本,我们将随机选取几个单词(例如每个单词被选中的概率为$10%$),并使用特殊的token UNK或者词表中任意一个token来代替。

这种方法背后的动机其实很简单:我们教会模型不应过分依赖单个token,而是要考虑整个文本的上下文。 在上图的例子中,我们将great掩盖,此时模型就需要学习基于其他单词来理解这段文本的情感(sentiment)。
Note: make use of a more global context.
这一点其实与图像中用色块掩盖图像部分区域的思想是一致的,即通过掩盖图像部分,迫使模型不应只依赖局部的特征,而是充分利用整个图像信息。
- 使用外部资源,例如同义词词典(thesaurus): 有点复杂
一种有点复杂的方法是使用其同义词替换单词或短语。棘手的部分在于如何这些同义词:对于英语,我们可以使用同义词词典(或者WordNet),然而除英语以外的其他语言很少使用。其次,对于一些形态丰富的语言(如俄语),简单的替换同义词有可能会违反语法规定。

- 借助外部模型: 甚至更复杂
更复杂的方法是使用外部模型解释整个句子。一种流行的释义方法是将句子翻译成某种语言然后再翻译回来,例如使用谷歌翻译、百度翻译等。需要注意的是,我们可以将翻译系统和语言结合起来以获取多个释义。

Note: 后两种方法对应图像中的几何变换:我们想要改变文本,但是要保留原有的含义。
这与单词丢弃不同,单词丢弃是将一些部分整个消除。
分析与可解释性
卷积可以学到什么东西?分析卷积过滤器
- 在计算机视觉中:卷积学习视觉模式
卷积最初是为图像而开发的,并且已经对不同类型的过滤器捕获了什么以及如何从不同层次结构的层中过滤有了很好的理解。虽然较低的层可以捕获简单的视觉图案(例如线条或圆圈),但最后一层可以捕获整个图片,如动物,人等。

◎ distill.pub上的实例
- 在文本中,卷积学到什么
对于图像,过滤器捕获对分类很重要的局部视觉模式。对于文本,此类局部模式为单词的n-grams。CNNs如何用于文本的主要发现如下:
- 卷积滤波器用作n-grams检测器
- 每个过滤器专注于一个或几个密切相关的n-gram家族
- 过滤器不是同质的,即一个过滤器可以检测多个明显不同的n-gram家族
- 最大池化:诱导阈值行为
- 进行预测时,低于给定阈值的值将被忽略(即不相关)。
- 该研究表明平均可以减少40%的池化n-gram,而不会降低性能。
了解网络捕获内容的最简单方法是查看哪些模式激活了其神经元。对于卷积,我们选择一个过滤器并找到最能激活该过滤器的n-grams(即过滤器获得的向量中值最大维度对应的n-grams)。
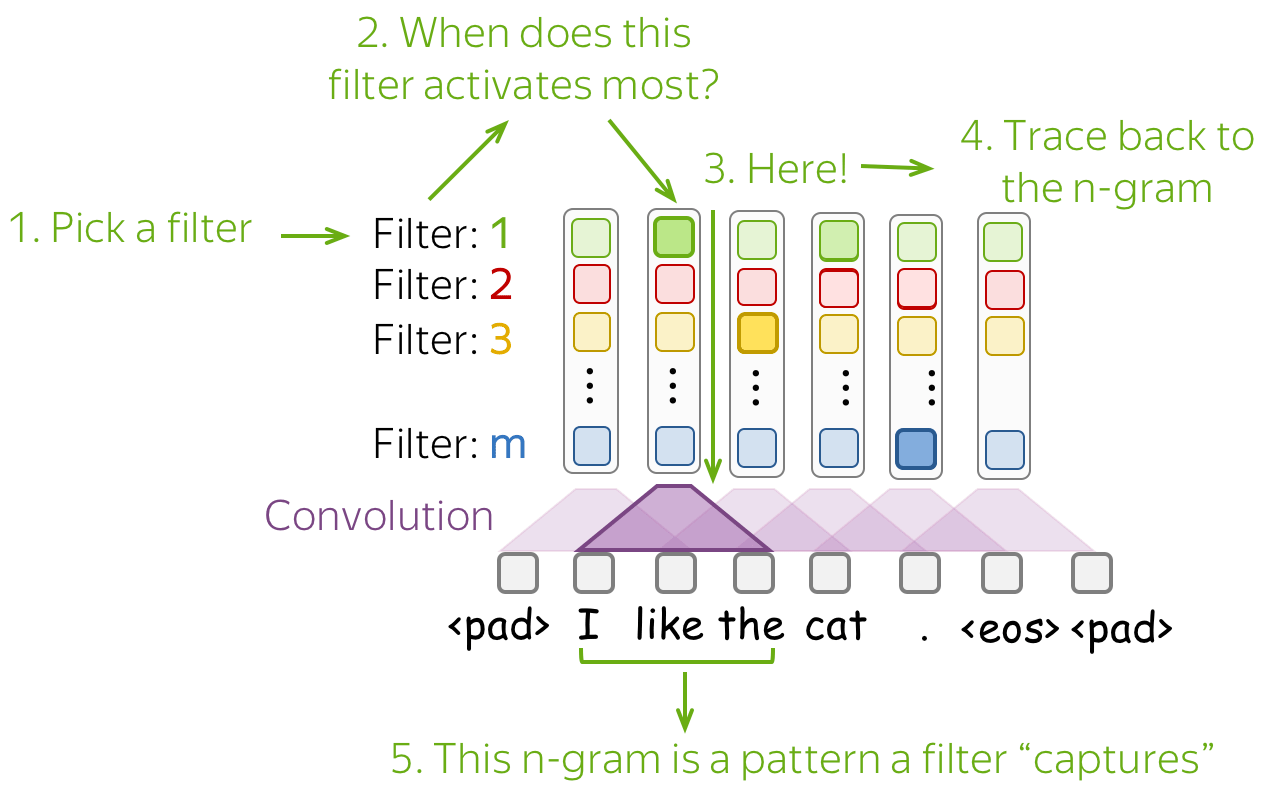
下图展示每个过滤器中激活得分最高的n-grams:

可以发现在过滤器4中,激活得分排名靠前的n-grams都有着非常相似的含义。
类比视觉中不同层次的卷积识别到不同层次的模式,在文本中,不同的卷积过滤器能识别到不同的n-grams模式,并且发掘对文本具有较高价值的n-grams以及其含义相近的n-grams家族。
研究反思
经典方法

最简单的朴素贝叶斯使用tokens作为特征,然而这并非总是好的方法,因为完全不同的文本也可以拥有相同的特征。
❓ 朴素贝叶斯最大的问题在于其对文本一无所知。当然我们不能移除“朴素”假设,否则就不再是朴素贝叶斯方法了。那么我们应该如何改进特征提取部分呢?
想法: 向特征中添加高频的n-grams!

除了单独使用单词作为特征,我们还可以使用单词的n-grams.由于使用所有的n-grams 会降低效率,那么我们可以只加入高频的n-grams.
❓ 还可以想出什么其他类型的特征?
注意到,朴素贝叶斯可以使用任何分类特征(categorical features)。我们可以执行任何操作,只要可以计算计数获得概率即可。
- 文本长度
- 有可能正面的评价可能比负面的评价更长。我们可以将长度为1-20的tokens组成一个特征,长度为21-30的tokens组成另一个特征,等等。
- token的频率
- 正面或负面评论可能使用更多奇怪的词。可以使用最少、最多、平均等统计特征表示token的频率
- 记得最终需要将特征做分类化(categorize)
- 句法(syntactical)特征
- 依赖树深度(最大/最小/平均),这可以代替文本的复杂性。
- 其他你想出的方法:Just try!
- 分类是否同等地需要所有单词?如果不是,我们如何修改该方法?
想法:不要使用不重要的单词。
如果我们知道哪些单词绝对不会影响分类的概率,那么我们可以将其从特征中移除。例如,我们可以移除停用词(stop-words): 确定词(determiners),介词(prepositions)等。

神经网络方法
❓ 对于微调后的嵌入,为什么以及什么时候会有用?
在训练模型之前,我们首先需要思考为什么微调会有用,以及哪一种类型的样本将会受益于微调。记住词嵌入是如何训练的:在文本中用法相近的单词具有非常相近的词嵌入。因此,有时反义词彼此最接近,例如descent和ascent。
想象我们想要使用词嵌入做情感分类。你能找到反义词的词嵌入非常紧密例子吗?如果有,这样的情况将会影响情感分类的结果?如果你找到这样的例子,这意味着最好要进行微调!
如果没有使用微调,那么最接近bad的词嵌入将是good!
下图显示了在使用微调的前后,Word2Vec中词嵌入最接近的几个单词。

如果不进行微调,模型将很难使用这些词嵌入来区分情感分类。微调还可以帮助提高对token的理解,例如n't: 这个单词在我们训练词嵌入的语料中很少见,但在我们关注的语料库中并不罕见。
更一般而言,如果我们的特定任务的训练数据与词嵌入的预训练数据不同,则微调是个好主意。


















