DEROOCE

NLP Notes series: Word Embeddings

 NLP/Word Embeddings  13034

Word Embeddings

背景

对于一段文本"I saw a cat",人类可以轻易理解其含义。然而，对于计算机模型却无法做到，它们需要特征向量(vectors of features),这样的向量，或者称“word embeddings"(词嵌入)可以作为文本的一种表示，并且模型也能够“理解”与处理这种表示。

然而，如何或者这种词嵌入表示呢？答案是：使用查找表(Look-up table),或者称词表(Vocabulary)。

在实践中，你有一个词表，其中包含着所有的许可词(allowed words),并且这个词表是提前选取好的。对于每一个词，查找表中都包含着其对应的嵌入表示，并且可以根据词在词表中的索引轻易地找到对应的嵌入表示,即根据词表中的索引，在查找表中寻找对应的嵌入表示。

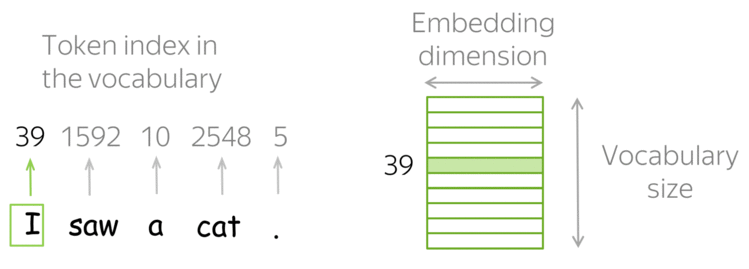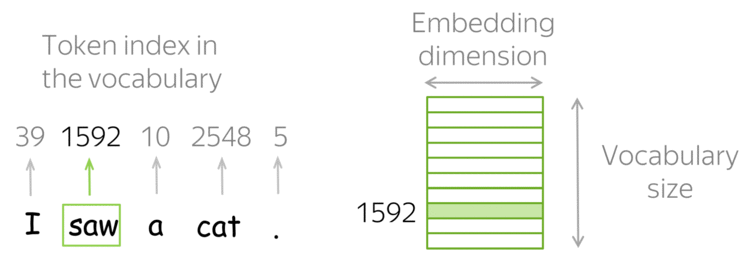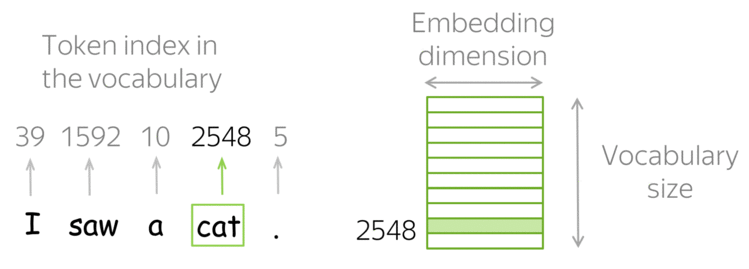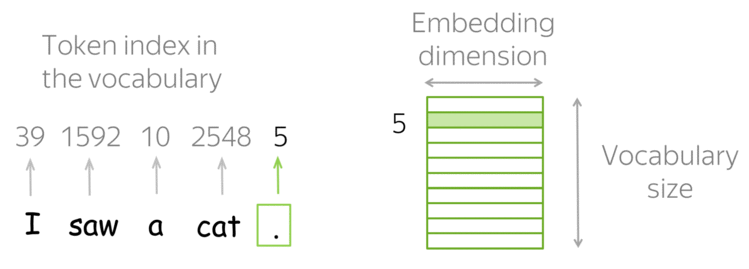◎ 词嵌入表示的查找

此外，考虑到存在未知的词,即那些不在词表中的词，通常一个词表中包含着一个特殊的词--UNK（unknown)。此外，未知词也可以直接忽略或是赋予一个0值向量。

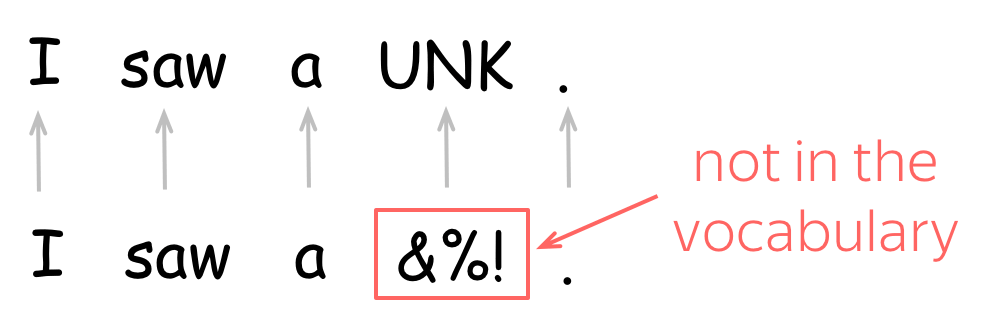
本文的主要目的就是：如何获得这些词嵌入向量(Word Embeddings)？

离散符号的表示：One-hot vectors

表示这些词的最简单方式就是使用独热编码(one-hot vectors): 词表的第$i$个词对应的表示向量中，除第$i$维的值为1外，其他维度的值都为0。在机器学习中，这也是表示分类特征的最简单方式。

然而，这样的表示存在许多问题：

  1. 当词表很大时，这些独热向量的维度也会非常大，即$d=|\mathcal{V}|$
  2. 这两个向量是正交的，独热向量无法表示对应词的任意信息

其中第二点是独热编码最大的缺点。例如，在词表中cat和dog的索引距离较近，因而独热编码也会认为cat和dog的意思相近，而这显然不合理。可以肯定地说，独热向量无法捕获词的含义。

但是我们如何知道词的含义呢？

分布式语义

为了捕获在这些向量中词的含义，我们首先需要定义在实践中可以被使用的含义记号。为此，先了解人类是如何理解哪些单词具有相似的含义。

◎ 分布式语义假设(Distributional Semantics Hypothesis)

一旦我们知道了在不同的上下文中，未知词是如何使用的，我们将有能力去理解该词的含义。

分布式假设: 频繁出现在相似语境的词之间有相似的含义。

根据分布式假设，我们的大脑将会搜索其他可以用于相同语境的词。在该例中，红酒(wine)一词符合该语境中的使用，因此，得到结论：tezgüino一词与wine具有相似的含义。

这个想法非常具有价值，甚至在实践中也可以被用来使词向量捕捉其词的含义。根据分布式假设，“捕获词的含义”和“捕获上下文”其实内在意义是相同的。因此，我们所要做的就是将词的上下文信息加入词的表示中,而获得的词向量其实就是词的分布式语义表示(distribution semantics representation)。

Main idea: We need to put information about word contexts into word representation.

J.R.Firth’s hypothesis from 1957, “You shall know a word by the company it keeps.”

本文主要阐述的也就是实现这种想法的不同方法。

Word Embeddings的性质

通过各种嵌入算法得到的词嵌入的简单性质：

  1. 余弦相似度 cosine similarity
    1. 为了估计词/上下文之间的相似性，通常我们需要衡量标准化(normalized)后的词/上下文向量的点积(dot-product),即余弦相似度(cosine similarity)。
    2. 两个词之间的相似度(在$[-1,1]$之间)
  2. 词嵌入可以通过线性代数解决词之间的类比关系(analogy relationships)
    1. 例如已知两个词man:woman,以及一个词king,寻找其对应的类比词
    2. 解法：寻找一个向量$w$，能够使得$v_{king}-w$与$v_{man}-v_{woman}$之间最相近，即最小化$||v_w - v_{king} + v_{man} - v_{woman}||^2.$
    3. 这种简单的思想可以在一些标准测试中解决$75\%$的词类比问题。

Embeddings模型需要关注的地方以及其作用

自然地，对于每个以词表中的单词作为输入，并将单词转换为向量嵌入到低维空间中，并通过反向传播算法微调的前馈神经网络，都必然会生成词的嵌入表示，并将其作为第一层的权重，这一层通常被称为嵌入层(Embedding Layer)[1]。

  • 网络方法：词的嵌入表示只是训练过程中的附带物(by-product)
  • Word2Vec方法：显式的目标就是生成词嵌入

而网络方法和Word2Vec类型方法的主要区别在于它们的计算复杂度。对于很大的词表，使用非常深的网络架构训练生成词嵌入很容易造成计算成本过大。这也是为什么直到2013年Word Embeddings研究才会在NLP领域爆炸性增长的原因--计算资源！ 计算复杂度是词嵌入模型的关键权衡点。

As a side-note, word2vec and Glove might be said to be to NLP what VGGNet is to vision, i.e. a common weight initialisation that provides generally helpful features without the need for lengthy training.

基于计数的方法

介绍

基于计数的方法(Counted-Based methods)手动地将全局语料库的统计信息加入到词表示中。

主要的步骤可以分为两步：

  1. 构建一个词的上下文矩阵
  2. 降低矩阵的维度

◎ 矩阵降维方法-SVD

降低维度的原因为：

  1. 初始的上下文矩阵会非常大
  2. 可能有很多词只出现在少量的上下文中，初始矩阵可能包含着很多无信息的元素，例如0元素

为了定义一个基于计数的方法，我们需要先定义两件事：

  • 什么是“词的上下文(contexts)”，以及什么是“词在上下文中的含义”
  • 关联(association)的概念，即计算上下文矩阵元素的公式

共现计数 Co-Occurrence Counts

Offconvex博客中提出的观点[2]：

All embedding methods try to leverage word co-occurence statistics.

◎ 词的上下文定义

共现计数是一种非常简单的计数方法。以每个词周围$L$长度的窗口作为其对应的上下文。上下文矩阵元素的定义为词$w$在上下文$c$中出现的次数$N(w,c)$。这是获得嵌入表示的最基础，并且非常古老的方法。

下面给出一个共现计数矩阵计算的实例：

co-occurrence matrix◎ 图片来源: Stanford cs224n slides

在上图中，假设窗口长度$L=1$,即每次只观察中心词左右两侧各1个单词长度的窗口，并统计该中心词在多个文本中，与其他单词共同出现在同一窗口的次数，并以该次数作为共现矩阵的对应元素值。

正点互信息: Positive Pointwise Mutual Information (PPMI)

在该方法中，上下文的定义方式与共数计数中的定义相同,但衡量词语上下文之间关联性的方式更加聪明：正PMI (PPMI)。PPMI曾一度被广泛认为是分布式-相似度(distributional-similarity)模型的最先进的度量方法。

令$p(w,w')$是词$w$在以$w'$为中心的5个单词组成的窗口内出现的经验概率，$p(w)$是词$w$在文本中出现的概率，$p(w')$是词$w'$在文本中出现的概率。则对应的点互信息(PMI)计算为: $$ PMI(w, w') = \log (\frac{p(w, w')}{p(w) p(w')}) \qquad \text{(Pointwise mutual information (PMI))} $$

🔥Important: 一些我们将会使用到的神经网络方法(如，Word2Vec)，隐式地近似（移位的，shifted）PMI矩阵的因式分解 $\color{#888}{u_{c}^T}{\color{#88bd33}{v_{w}}} =PMI(\color{#88bd33}{w}, \color{#888}{c}-\log k)$,其中$k$表示负采样的样本个数。

潜在语义分析 Latent Semantic Analysis (LSA): Understanding Documents

潜在语义分析(LSA)分析文件集合。在之前的方法中，上下文的作用仅是为了获得词向量，用完之后就会被抛弃。然而。在LSA中，上下文仍然被作为关心的信息，或者在该方法中称为文档向量(document vectors)。LSA是最简单的主题模型(topic models)之一:文档向量之间的余弦相似度用于衡量文档之间的相似性。

“LSA”有时指代对一个文档矩阵(term-document matrix)应用SVD的更广泛的方法。文档矩阵的元素可以使用不同方式计算，例如简单的共现计数、tf-idf或者其他权重方法。

基于预测的方法：Word2Vec

原理

首先，我们不要忘记这些方法的主要依据思想：将上下文中的信息加入到此向量中。

基于计数的方法很好地体现了主要依据思想，而Word2Vec从另一个方式体现：通过教模型预测上下文来学习词向量。

How: Learn word vectors by teaching them to predict contexts.

Word2Vec的参数为词向量。这些参数针对特定目标进行了迭代优化。这个目标迫使词向量理解词应该出现在什么样的上下文中：对向量进行训练以预测相应单词的可能上下文。如果还记得我们的分布式假设，如果词向量能理解上下文，那么这些向量也就能知道词的含义。

Word2Vec是一种迭代的方法，它的主要思想如下：

  1. 使用一个巨大的预料库
  2. 通过一个滑动窗口遍历所有的文本，窗口每次移动一个单词。在每一步，都有一个中心词(center word)和上下文词(context words)
  3. 对于中心词，计算其对应的上下文词的概率
  4. 调整词向量，增加上下文词的概率

◎ Word2Vec计算流程示意

目标函数：负对数似然

对于文本预料的每个位置$t=1,...,T$, 给定中心词$\color{#88bd33}{w_t}$,Word2Vec将根据一个$m$-大小的窗口来预测上下文词: $$ {\color{#88bd33}{\text{Likelihood}}}= L(\theta)= \prod\limits_{t=1}^T\prod\limits_{-m\le j \le m, j\neq 0}P(\color{#888}{w_{t+j}}|\color{#88bd33}{w_t}, \theta), $$ 其中$\theta$是所有需要优化的变量。目标函数(aka. 损失函数、成本函数)$J(\theta)$是平均负对数似然： ◎ 似然函数取对数

注意，负对数似然函数与我们所期望的目标的相符程度: 使用一个滑动窗口遍历整个文本，并且计算上下文的概率值。现在，我们来弄清楚如何计算概率值$P(\color{#888}{w_{t+j}}\color{black}|\color{#88bd33}{w_t}\color{black}, \theta)$：

对每个词$w$,我们将会获得两个向量：

  • $\color{#88bd33}{v_w}$: 当$w$是中心词时
  • $\color{#888}{u_w}$： 当$w$是上下文词时

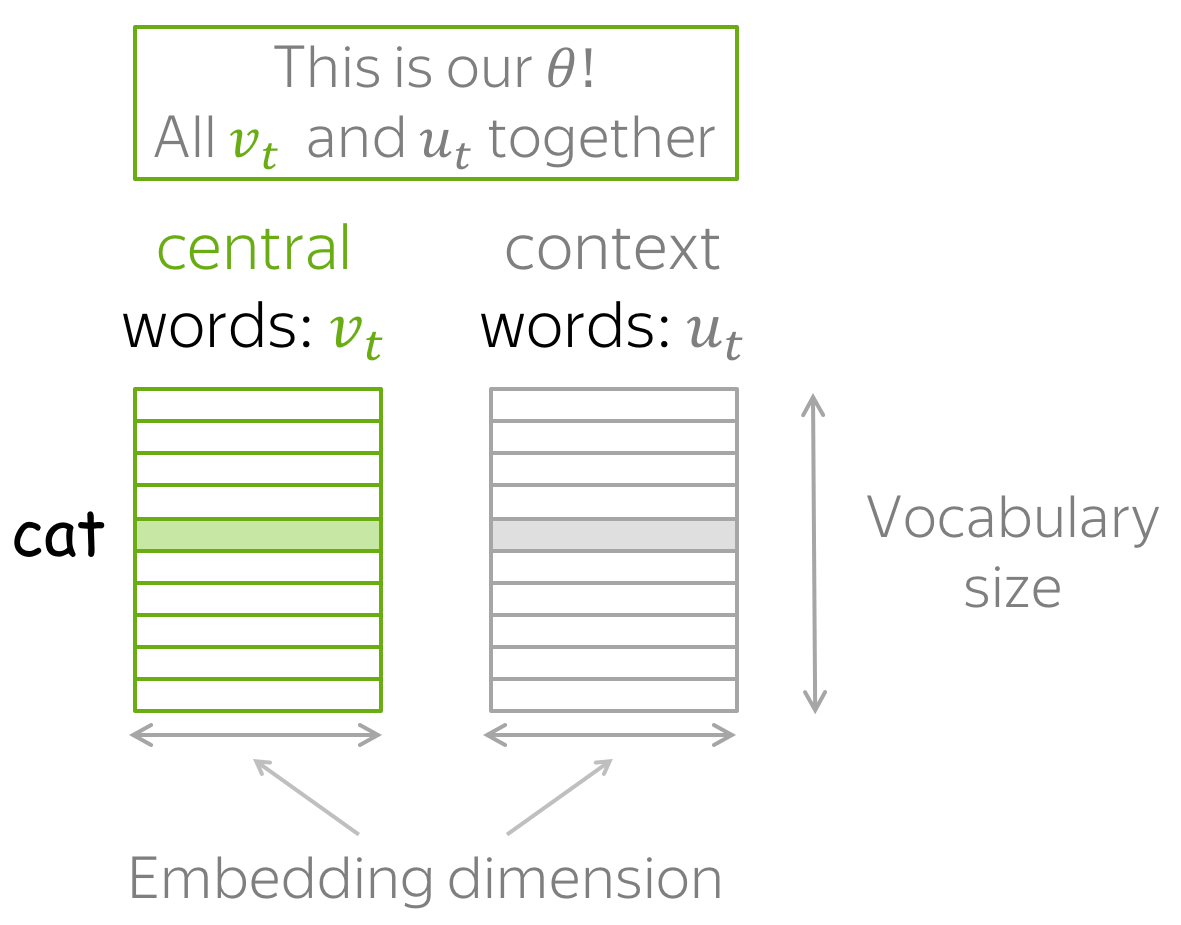
一旦向量经过训练后，通常我们将会丢弃所有的上下文词向量，而保留词向量。

对于中心词$\color{#88bd33}{c}$ (c-central)，上下文词$\color{#888}{o}$ (o-outside)以中心词为条件的条件概率为：

一个词将用有两个向量对应:$u,v$,而在网络训练学习这些词嵌入时，这些向量首先随机初始化，赋予它们一个初值，然后根据后续的优化算法逐步学习出一个好的嵌入向量。

注意到上述的函数形式其实就是softmax函数$\mathbb{R}^n\rightarrow \mathbb{R}^n$： $$ softmax(x_i)=\frac{\exp(x_i)}{\sum\limits_{j=i}^n\exp(x_j)}. $$

Softmax函数将任意的值$x_i$映射成一个概率分布$p_i$:

  • "max"表示最大的$x_i$值将会有最大的概率值$p_i$
  • "soft"表示所有的概率都非零,即使是一些小的$x_i$值也会被赋予一定的概率值

中心词：central words和上下文词：context words，下面将给出一个图例帮助理解整个概率值的生成过程。假设第一个中心词是$a$,将其记为$\color{#88bd33}{v_a}$，而当窗口滑动，$a$成为上下文词时，将其记为$\color{#888}{u_a}$。

◎ 条件概率的生成示例

如何训练

梯度下降

通过梯度下降，一次更新一个词

回忆我们所需学习的参数$\theta$为词表中所有词的$\color{#88bd33}{v_w}$和$\color{#888}{u_w}$。通过对目标函数使用梯度下降算法来学习这些词向量参数： $$ \theta^{new} = \theta^{old} - \alpha \nabla_{\theta} J(\theta). $$

需要注意的是$\theta$表示的是模型的所有参数。对于一个大小为$|V|$的词表，每个嵌入向量维度为$d$,而这些向量都将包含在$\theta$内，如下图所示：

一次更新一个词：每次只更新一个(中心词-上下文词)配对。损失函数为：

$$ \begin{aligned} \color{#88bd33}{\mbox{Loss}}\color{black} =J(\theta)= -\frac{1}{T}\log L(\theta)&= -\frac{1}{T}\sum\limits_{t=1}^T \sum\limits_{-m\le j \le m, j\neq 0}\log P(\color{#888}{w_{t+j}}\color{black}|\color{#88bd33}{w_t}\color{black}, \theta) \\&= \frac{1}{T} \sum\limits_{t=1}^T \sum\limits_{-m\le j \le m, j\neq 0} J_{t,j}(\theta). \end{aligned} $$

对于每个中心词$\color{#88bd33}{w_t}$,损失函数包含一个与其上下文词$\color{#888}{w_{t+j}}$对应的项$J_{t,j}(\theta)=-\log P(\color{#888}{w_{t+j}}\color{black}|\color{#88bd33}{w_t}\color{black}, \theta)$.

为理解整个训练过程，先看一个例子。对于如下序列语句： 中心词为$\color{#88bd33}\mathrm{cat}$,以及含有四个上下文词。在训练时，我们先从中选出一个上下文词，假设选择$\color{#888}\mathrm{cute}$,那么这个($\color{#88bd33}\mathrm{cat}$,$\color{#888}\mathrm{cute}$)配对的损失函数项为:

$$ \begin{aligned} J_{t,j}(\theta)= -\log P(\color{#888}{cute}\color{black}|\color{#88bd33}{cat}\color{black}) &= -\log \frac{\exp\color{#888}{u_{cute}^T}\color{#88bd33}{v_{cat}}}{ \sum\limits_{w\in Voc}\exp{\color{#888}{u_w^T}\color{#88bd33}{v_{cat}} }} \\ &= -\color{#888}{u_{cute}^T}\color{#88bd33}{v_{cat}}\color{black} + \log \sum\limits_{w\in Voc}\exp{\color{#888}{u_w^T}\color{#88bd33}{v_{cat}}}\color{black}{.} \end{aligned} $$
$$ \begin{aligned} \frac{\partial}{\partial v_c}(u_0^Tv_c)-\frac{\partial}{\partial v_c}\log \sum_{w\in Voc}\exp (u_o^Tv_c)&=u_o-\sum_{x=1}^{V}\frac{\exp(u_x^Tv_c)}{\sum_{w\in Woc}\exp(u_w^Tv_c)}\cdot u_x\\ &=u_o-\sum_{x=1}^{V}p(x|c)\cdot u_x \end{aligned} $$

现在注意到该步的参数：

  • 中心词的词向量参数: $\color{#88bd33}{v_{cat}}$
  • 上下文词的词向量参数：所有的$\color{#888}{u_w}$（词表中的所有词）

只有这些参数在当前训练步上需要更新。更新步骤有如下图示：

为了更新参数以最小化损失函数项$J_{t,j}(\theta)$,我们需要强制增加$\color{#88bd33}{v_{cat}}$和$\color{#888}{u_{cute}}$的相似度(即点积)，并同时降低$\color{#88bd33}{v_{cat}}$和词表中所有词$w$的上下文词$\color{#888}{u_{w}}$之间的相似度。 ◎ 训练策略

但是这里可能会出现一个疑问：为什么还需要降低$\color{#88bd33}{v_{cat}}$和其他所有词之间的相似度？ 如果其他词中也包括有效的上下文词（例如该例中的$\color{#888}\mathrm{grey,playing}$等）,这样做岂不是会降低其他上下文词预测的概率吗？

但我们其实不必担心：因为我们会对每个上下文词都进行更新,在在本次更新中，降低相似度的上下文词会在另一些更新中 增加其相似度。于是平均而言，在所有的更新结束后，最终优化后的向量会学习到可能的上下文词的分布。

更快的训练方式：负采样

Negative Sampling

在之前的例子中，对于每个(中心词,上下文词)配对，我们都需要更新所有的上下文词向量。这样会导致显著的低效率性，每一步的计算时间复杂度都与词表的大小成正比。

因此，我们将会产生疑惑：为什么一定要在每一步中都更新所有的上下文词向量？举例来说，假设在当前步，我们不考虑所有词的上下文词，而只考了当前(中心词，上下文词)配对中的上下文词(上例中是$\color{#888}\mathrm{cute}$)以及随机选择词表中的几个词。下图将展示这个想法： ◎ 负采样方法只随机选取K个词

与梯度下降算法中一样，我们更新都需要提高$\color{#88bd33}{v_{cat}}$和$\color{#888}{u_{cute}}$的相似度，但不同的是，在负采样方法中，我们不需要降低$\color{#88bd33}{v_{cat}}$与所有词的上下文词之间的相似度，而只需随机选择词表中大小为$K$的"负”(negative)词，并降低其与中心词间的相似度。

因为我们具有很大的语料数据，因此平均所有的更新而言(on average over all updates)，即使每一步不使用所有的上下文词更新，只要我们更新的次数足够多，最终学习到的词向量也能很好地学习到此之间的关系。

如果需要正式地说明，当前步的新损失函数可以表达为： $$ J_{t,j}(\theta)= -\log\sigma({\color{#888}{u_{cute}^T}\color{#88bd33}{v_{cat}}}) - \sum\limits_{w\in {w_{i_1},\dots, w_{i_K}}}\log\sigma({-\color{#888}{u_w^T}\color{#88bd33}{v_{cat}}}), $$ 其中$w_{i_1},\dots, w_{i_K}$表示在当前步上随机选择的$K$个负样本，以及$\sigma(x)=\frac{1}{1+e^{-x}}$表示sigmoid函数。

注意到$\sigma(-x)=\frac{1}{1+e^{x}}=\frac{1\cdot e^{-x}}{(1+e^{x})\cdot e^{-x}} = \frac{e^{-x}}{1+e^{-x}}= 1- \frac{1}{1+e^{x}}=1-\sigma(x)$,因此损失函数还可以改写为：

$$ J_{t,j}(\theta)= -\log\sigma({\color{#888}{u_{cute}^T}\color{#88bd33}{v_{cat}}}) - \sum\limits_{w\in {w_{i_1},\dots, w_{i_K}}}\log(1-\sigma({\color{#888}{u_w^T}}\color{#88bd33}{v_{cat}})). $$

关于负采样的几点说明：

  1. 由于滑动窗口大小的限制，每个中心词只对应着几个“正”上下文词。因此，随机选择的词很可能并不是真正上下文词中的一个，因此称其为"负“(negative)样本
    1. 这种采样的思想不仅在Word2Vec中得到使用，其他应用中也存在这种思想
  2. Word2Vec根据词的经验分布(empirical distribution)来随机选择负样本
    1. 假设$U(w)$是一个一元模型分布（unigram distribution），即$U(w)$表示此$w$在文本语料中出现的频率
    2. Word2Vec通过对这种分布进行调整，使得在语料中出现频率少的词被选中的概率增加,而改良后的一元模型分布形式为$U^{3/4}(w)$,将其称为平滑一元模型分布(Smoothed unigram distribution)

如果将改进后的分布具体写出，则其形式如下： $$P\left(w_{i}\right)=\frac{f\left(w_{i}\right)^{3 / 4}}{\sum_{j=0}^{n}\left(f\left(w_{j}\right)^{3 / 4}\right)}$$ 其中$f(w_i)$表示词在文本语料中出现的频率。

改进分布中的$3/4$是有实验经验获得的结果，在实验中,指数选择$3/4$的效果最佳。

后加工

加入上下文向量

Adding context vectors: GloVe的作者建议将词向量和上下文向量合并一起作为最终的输出向量，即$\vec{v}_{\text{cat}} = \vec{w}_{\text{cat}} + \vec{c}_{\text{cat}}$。这样输出增加了一阶相似度， 即$w\cdot v$。

然而，该处理不能被应用与PMI(点互信息)，因为PMI生成的向量是稀疏的。

向量标准化

将所有向量归一化.

推荐训练技巧

Takeaways[3]

  • DON'T use shifted PPMI with SVD.
  • DON'T use SVD "correctly", i.e. without eigenvector weighting (performance drops 15 points compared to with eigenvalue weighting with p=0.5).
  • DO use PPMI and SVD with short contexts (window size of 22).
  • DO use many negative samples with SGNS.
  • DO always use context distribution smoothing (raise unigram distribution to the power of $\alpha$=0.75) for all methods.
  • DO use SGNS as a baseline (robust, fast and cheap to train).
  • DO try adding context vectors in SGNS and GloVe.

Word2Vec变种：Skip-Gram和CBOW

  • Skip-Gram: 与Word2Vec的主体思想一致，即给定中心词来预测其上下文词。使用负采样更新的Skip-Gram模型(Skip-Gram with Negative Sampling,SGNS)是最常用的方法之一
    • SGNS: 隐式地近似(偏移 shifted)PMI矩阵的因式分解
  • CBOW(Continuous Bag-of-Words): 与Word2Vec思想恰好相反，根据上下文词向量的累加和来预测中心词，而这种简单的词向量累加结果称为Bag of words,CBOW模型也是因此得名

◎ Skip-Gram vs. CBOW

额外笔记

The Idea is Not New: 这种根据上下文词学习中心词的想法其实不是特别新的想法，然而Word2Vec出人意料的地方在于其可以学习到高质量(high-quality)的词向量，以及可以在很大的语料数据集和词表中非常快速地学习。

Why Two Vectors?: 回忆Word2Vec中的内容，我们需要训练两个向量：中心词向量和其对应的上下文向量，并且在训练结束后，上下文词向量将会直接丢弃，不需再使用，那么为什么还需要使用两个向量? 其实这就使得Word2Vec模型简单高效的技巧所在。我们再看一下某一步更新的损失函数： $$ J_{t,j}(\theta)= -\color{#888}{u_{cute}^T}\color{#88bd33}{v_{cat}} - \log \sum\limits_{w\in V}\exp{\color{#888}{u_w^T}\color{#88bd33}{v_{cat}}}{.} $$ 当中心词和上下文词使用不同的向量，在损失函数（负采样方法中的损失函数也是同理）的第一项和第二项指数内的点积其实都关于参数(即词向量)是线性的，因此梯度可以非常容易地计算，从而训练速度也会非常快。

滑动窗口的大小选择: 滑动窗口的大小对向量相似度的计算有很大的影响。有研究表明：越大的窗口越能产生主题相关的相似度(topical similarities),例如walked,run,walking等词会分类在一起，词向量会比较接近；而越小的窗口越能产生更多功能与句法(functional and syntactic)上的相似度，例如Walking,running,approaching等。

某种程度上的标准超参数设置: 通常超参数的选择取决于需要解决的任务，不过根据一些研究的经验，得到某种程度上的一个标准：

  1. 模型选择: 使用负采样的Skip-Gram模型
  2. 负采样的个数：
    1. 小数据集：15-20个采样样本
    2. 大数据集： 2-5个采样样本
  3. 嵌入表示的维度：通常选择的维度大小为300维，但是其他变种，如50或100也可能有效
  4. 滑动窗口的大小：5-10

Glove: Global Vectors for Word Representation

Glove模型(全局向量)是基于计数的方法和基于预测的方法的结合。Glove表示Global Vectors,其反映的思想是：使用整个文本语料的全局信息来学习词向量。

在之前章节,最简单的基于计数的方法采用共现计数来衡量中心词$\color{#88bd33}w$和上下文词$\color{#888}c$之间的关联度$N({\color{#88bd33}w},{\color{#888}c})$。Glove也使用该计数方法构建其损失函数：

与Word2Vec思想相似，Glove也需要学习中心词向量和上下文词向量。此外，Glove还分别对两个向量加入了偏置项，而偏置项也同样是需要学习的参数。

Glove中非常有趣的一个地方在于其控制出现频率低的词和出现频率高的词对损失函数影响大小的方式：在损失函数中，每个中心词-上下文词配对$({\color{#88bd33}w},{\color{#888}c})$对损失函数的影响都会有一个对应的权重。

  • 出现频率低的词将会被惩罚
  • 出现频率高的词也不会有过于大的权重

词嵌入表示的评估

我们如何评估一个方法获得的词嵌入表示比另一个方法的效果好坏呢？通常有两种评估方法（不仅适用于词嵌入的评估）：内部任务评价（Intrinsic Evaluation）和外部任务评价（extrinsic evaluations）。

内在任务评价: 基于内在的属性

这种评价方法着眼于嵌入的内在属性，例如这些词嵌入捕获词的含义的能力好坏。

  • 在特定或中间子任务上进行评估
  • 计算速度快
  • 可以帮助理解系统
  • 除非建立与实际任务的相关性，否则无法明确是否真的有用

外在任务评价: 在真实任务中测试

这种评估方法可以检验哪种嵌入更适合真正关心的任务，例如文本分类等。在这种评估方法中，我们需要在真实任务中，训练多次模型/算法：一个模型获得一个对应的词嵌入，接着，检查这些模型的性能来决定哪个词嵌入更好。

  • 在真实任务中评估
  • 可能需要很长时间计算准确率
  • 无法明确问题出现在子系统还是子系统之间的相互作用
  • 如果将一个子系统替换为另一个子系统可以提高准确率->这样做就是行得通的！

如何选择

在此之前，我们应该知道在所有的情形中，并不存在什么完美方法以及正确的解答。

对于评估方法，我们通常关注地是我们想要解决任务的质量(quality)。因此，我们更可能倾向于使用外在任务评估。然而在真实任务中，模型通常需要很多时间和资源来训练，而训练多个模型更是成本太高。

总而言之，这需要看你自己的能力（你的资源）来决定 :)

分析与可解释性

本节将重点关注模型在训练过程中学习到了什么，即模型解释性的问题。

语义空间

语义空间专注于创造捕获自然语言含义的表示。我们可以说（好的）词嵌入形成了语义空间，并将多维空间中的一组词向量称为“语义空间”。

下图将展示使用twitter数据获得的Glove向量组成的语义空间。向量使用t-SNE映射到2维空间中，并只展示前3k个最常见的单词。

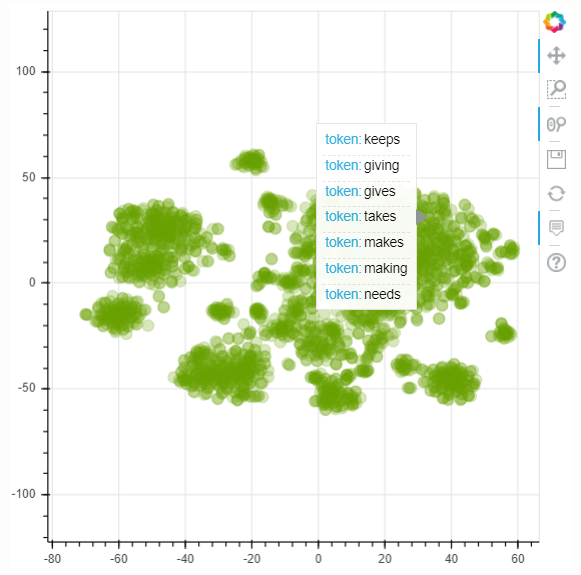
最近邻

在语义空间中，距离较近的点（向量）通常具有相近的含义。有时，即使是一些极少出现的词也能很好地理解。例如下图所示，leptodactylidae和litoria非常接近于frog。

◎ GloVe项目上的例子

词相似度基准

通过余弦相似度或欧式距离来获得最近邻，查看最近邻是估计词表示质量的常用方法之一。有几个单词相似性基准（测试集），它们由根据人类的判断具有相似性分数的单词对组成。词嵌入的质量使用两个相似性得分（来自模型和来自人类）之间的相关性来估计。

线性结构

尽管词相似度的结果令人鼓舞，但并不令人惊讶：毕竟，词嵌入本意就是通过专门的训练来反映单词的相似度。然而，令人惊讶地是词之间的许多语义和句法关系在词向量空间中（几乎）是线性的。

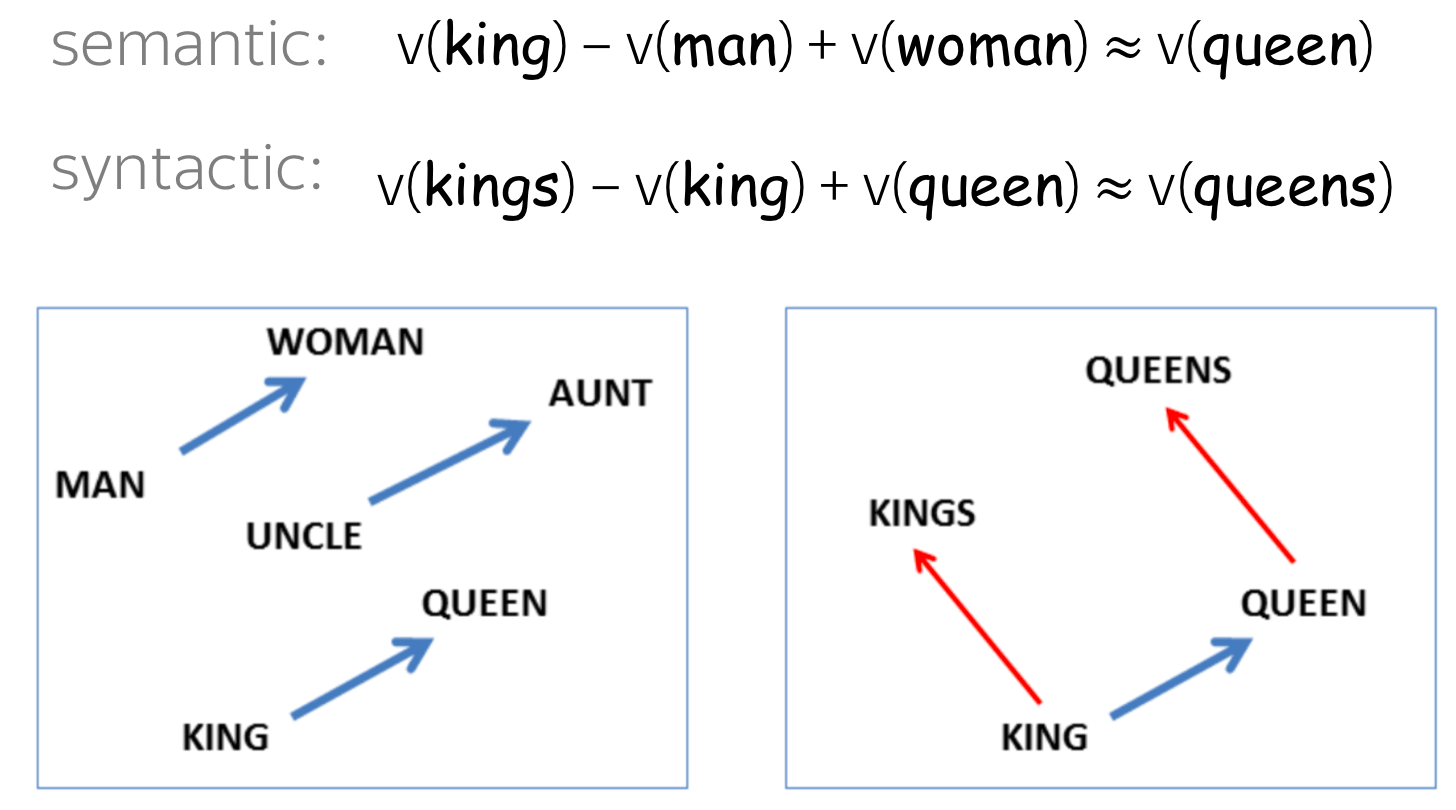
上图就显示了这种线性关系。king和queen之间的距离几乎与man和woman之间的距离相同，可以说$\mathrm{man-woman}\approx \mathrm{king-queen}$；又或是kings与king相似，则同样也有queens和queen。

下图的例子显示了国家-首都的关系，以及一些句法上的关系。

词类比基准

这种词向量之间的(近乎)线性关系启发了一种新的评价方法：词类比评估(word analogy evaluation)。 ◎ 类比词任务

给定相同关系的两个单词对,例如(man,woman)和(king,queen)，任务是检测我们是否能根据三个单词来识别剩余的一个单词。具体来说，我们需要检测与向量$\mathrm{king-man+woman}$最接近的向量是否是$\mathrm{queen}$。

几个类比基准数据：these include the standard benchmarks (MSR + Google analogy test sets) and BATS (the Bigger Analogy Test Set).

跨语言的相似度

在之前的小节中，我们知道在词嵌入空间中，词向量的关系是(近乎)线性的。然而，当跨语言时将会发生什么？结果表明，语义空间之间的关系也在某种程度上是线性的：你可以将一个语义空间线性地映射到另一个语义空间，以使两种语言中的相应单词在新的联合语义空间中匹配。

◎ 两种语言中的对应单词配对

The figure above illustrates the approach proposed by Tomas Mikolov et al. in 2013 not long after the original Word2Vec.

在形式上，给定一组词配对以及它们的向量表示配对${\color{#88a635}{x_i}\color{black}, \color{#547dbf}{z_i}\color{black} }_{i=1}^n$,其中$\color{#88a635}{x_i}$和$\color{#547dbf}{z_i}$分别是源语言(source language)中的第$i$个词，以及目标语言(target language)中对应的翻译单词。我们希望找到一个映射矩阵$W$，使得$W\color{#547dbf}{z_i}$近似于$\color{#88a635}{x_i}$,也即从两个语言的字典中找到匹配的单词。

我们将根据如下准则选取$W$: $$ W = \arg \min\limits_{W}\sum\limits_{i=1}^n\parallel W\color{#547dbf}{z_i} - \color{#88a635}{x_i}\parallel^2, $$ 并且通过梯度下降算法优化。

在原始论文中，初始对应的词表由5k个常见的单词与其对应的翻译组成，剩下的单词翻译配对将由学习得到。然而在之后的研究中表明，我们根本不需要建立字典，即使我们对语言一无所知，我们也可以在语义空间之间建立映射！

这种对不同的嵌入式表示集合进行线性映射以进行集合中元素匹配的想法可以被应用到许多不同任务中。

❓ 语言之间的“真实”映射是否确实是线性的或更复杂？

在一些研究中发现，我们可以根据学习到的语义空间的几何特性进行检验。

问题探讨 Rethinking

问题1

❓ 与中心词距离不同的上下文词对中心词是同等重要的吗？如果不是，如何改进 共现计数方法？

在直觉上，与中心词越接近的上下文词应该更加重要一些。例如，比起距离3的单词，近邻的信息量更大。因此，我们可以改进这个模型：当计数时，给距离中心词更近的上下文词更多的权重。

This idea was used in the HAL model (1996), which once was very famous.

问题2

❓ 在语言中，词的出现顺序很重要，具体来说，左右的上下文词具有不同的含义。我们应该如果区分左右上下文词呢？

当需要区分左右上下文词时，修改权重的方法将不再有效，因为我们不能断言左边还是右边的上下文词更重要。我们所需做的是分别计算左边和右边的共现次数。

对每个上下文词，我们都有两种不同的计数：

  1. 当该上下文词处于中心词左边时
  2. 当该上下文词处于中心词右边时

这意味着共现计数矩阵的大小应为$|V|\times 2|V|$。

This idea was also used in the HAL model (1996).

问题3

❓ 所有的上下文词都是同等重要的吗？是否存在某些类型的上下文词能比其他类型的上下文词提供更多的信息？考虑有哪些特征可以影响上下文词的重要性。

  1. word frequency : 词出现的频率
    1. 我们可以预期，与罕见词相比，常见词通常所提供的信息更少。
    2. E.g: 在上图例子中，in为cat的上下文词并出现多次，然而in同时也作为其他很多词的上下文词，却没有提供有用信息。然而，例如cute、grey和playing这些出现较少的上下文词，却提供了一些关于cat的特征信息
  2. Distance from the central word: 上下文词与中心词的距离
    1. 正如我们在问题1中讨论的，越接近中心词的上下文词可能越重要

问题4

❓ 我们应该如何改进训练过程?

  • 根据词的频率

由问题3中得到的启发，我们考虑出现频率低和出现频率高的词所带来的信息量。Word2Vec使用了一个简单的下采样(subsampling)方法：在训练集中的每个词$w_i$，都以一定的概率被忽略。忽略概率值计算如下： $$ P(w_i)=1 - \sqrt{\frac{thr}{f(w_i)}} $$

其中$f(w_i)$表示词$w_i$出现的频率，$thr$表示选择的阈值(在Word2Vec原始论文中，采用$thr=10^{-5}$)。该等式保留了词出现频率的排序，但对出现频率大于阈值$thr$的词积极地进行了下采样。

有趣的是，这种启发式方法在实践中效果很好：它加快了学习速度，甚至显着提高了出现频率低的单词的学习向量的准确性。

  • 根据与中心词的距离

在之前的问题中中，我们给距离中心词近的上下文词赋予了更大的权重。乍一看，在原始Word2Vec实现中并没有体现出任何权重调整。然而，在每一步中，它都从$1$到$L$采样上下文窗口的大小。因此，距离中心词近的词将会比距离远的词得到更多的采样。在原始工作中，这样做（可能）是为了提高效率（每个步骤的更新次数较少），但这也与分配不同权重具有相似的效果。

问题5

通常在查询表(look-up table)中，每个词都被赋予一个对应的向量。通过构造，这些向量对它们组成的子词(subwords)一无所知：它们拥有的所有信息都是从上下文中学到的。

❓ 如果词嵌入对它们组成的子词有一定的了解，这样会带来什么好处？

  • 更好地了解词的形态(morphology)，例如动词时态
    • 通过给每次词赋予不同的向量，我们这时就忽略了单词的形态。
    • 如果给定了子词的信息，那么模型就能发掘一些不同的词其实是由同一个词组成的
  • 未知单词的表示
    • 通常我们只表示存在于词表中的词
    • 如果给定子词的信息，将有助于未知词的拼写来表示这些未知词
  • 处理拼写错误
    • 即使单词中只有一个字符出错，那也将会成为另一个单词，因此也就会学习到一个完全不同的嵌入表示(甚至是一个未知词的嵌入表示)
    • 如果给定子词的信息，则拼写错误的单词的嵌入表示也将会和原始单词的嵌入表示相近

问题6

❓ 我们如何将子词的信息整合进词的嵌入表示（例如使用负采样的Skip-Gram）中？

假设训练流程是固定的，例如采用SGNS(Skip-Gram with Negative Sampling)。

一种可能的方法是使用子词的向量来组成该词的词向量。例如，流行的 FastText embeddings，对每一个词，都添加特殊的起始字符(start characters)和终止字符(end characters)；接着，除了使用该原始词的词向量，FastText也使用字符n-grams(characters n-grams)的向量，而这些字符n-grams也在词表中存在；最终，原始词的词嵌入表示由该词的词向量和子词的词向量的累加组成的向量构成。

注意，这种方法仅改变了我们形成单词向量的方式。整个训练流程与标准的Word2Vec相同。

问题7

假设我们有一个从不同来源组成的文本语料：时间段(time periods)，人口(populations)，地理区域(geographic regions)等。在数字人文科学(digital humanities) 和计算社会科学(computation social science)中,人们通常想找到在这些语料中语法不同的单词。

❓ 给定两个语料，我们如何检查一个单词在这两个语料中的含义/用法是否不同？

  • ACL 2020: train embeddings, look at the neighbors

一种非常简单的方法是训练嵌入表示（例如Word2Vec）并查看最近邻。如果一个单词在两个语料中的最近邻不相同，则判断该词在两个语料中的含义不同。

请记住，词嵌入反映了它们所处的上下文！如果词嵌入都不同，那么上下文含义也不同，那么也反映该词在不同的上下文中的含义也不相同。

这个方法在 ACL 2020 paper中被提出。正式地，对于每个单词，作者都在两个嵌入集合中选择$k$个最近邻的嵌入，并且计算这两个最近邻集合中有多少个相同元素。大交集意味着该单词的含义在两个语料中没有不同，小交集意味着含义不同。

  • Previous popular approach: align two embedding sets 对齐两个嵌入集

在之前的研究中，对齐两个嵌入集并找到嵌入不匹配的单词。在形式上，令$\color{#88a635}{W_1}\color{black}, \color{#547dbf}{W_2}\color{black} \in \mathbb{R}^{d\times |V|}$为在不同语料中训练得到的嵌入集合。为了对齐学习到的嵌入，作者找到一种旋转方法(rotation)$R = \arg \max\limits_{Q^TQ=I}\parallel \color{#547dbf}{W_2}\color{black}Q - \color{#88a635}{W_1}\color{black}\parallel_F$,这被称为$\mathrm{Orthogonal ~~Procrustes}$(正交普鲁克).

普鲁克问题：

$$ W^{*}=\operatorname{argmin}_{W} \sum_{i=1}^{n}\left\|W x_{i}-y_{i}\right\|_{2} $$

or

$$ W^{*}=\arg \min _{W}\|W X-Y\|_{F} $$

普鲁克：在希腊神话中，Procrustes或“the stretcher”是来自Attica的流氓史密斯和强盗，他们通过拉伸或切断腿部来攻击人们，以迫使他们适应铁床(iron bed)的大小。

我们使用原嵌入空间来做同样“糟糕”的事情。我们的Procrustean床是目标嵌入空间。

通过使用这种旋转，我们可以将嵌入集合对齐，并且找到没有对齐的单词，而这些没有对齐的单词表示在不同语料中的含义发生了改变。

Reference

  1. Lena Voita: word_embeddings
  2. Sebastian Ruder Blog
  3. offconvex: word embedding
  4. Stanford cs224n

  1. Sebastian Ruder: On word Embeddings - Part 1 ↩︎

  2. Offconvex: Word Embedding ↩︎

  3. Sebastian Ruder: On word Embeddings - Part 3 ↩︎

updatedupdated2022-08-202022-08-20
加载评论